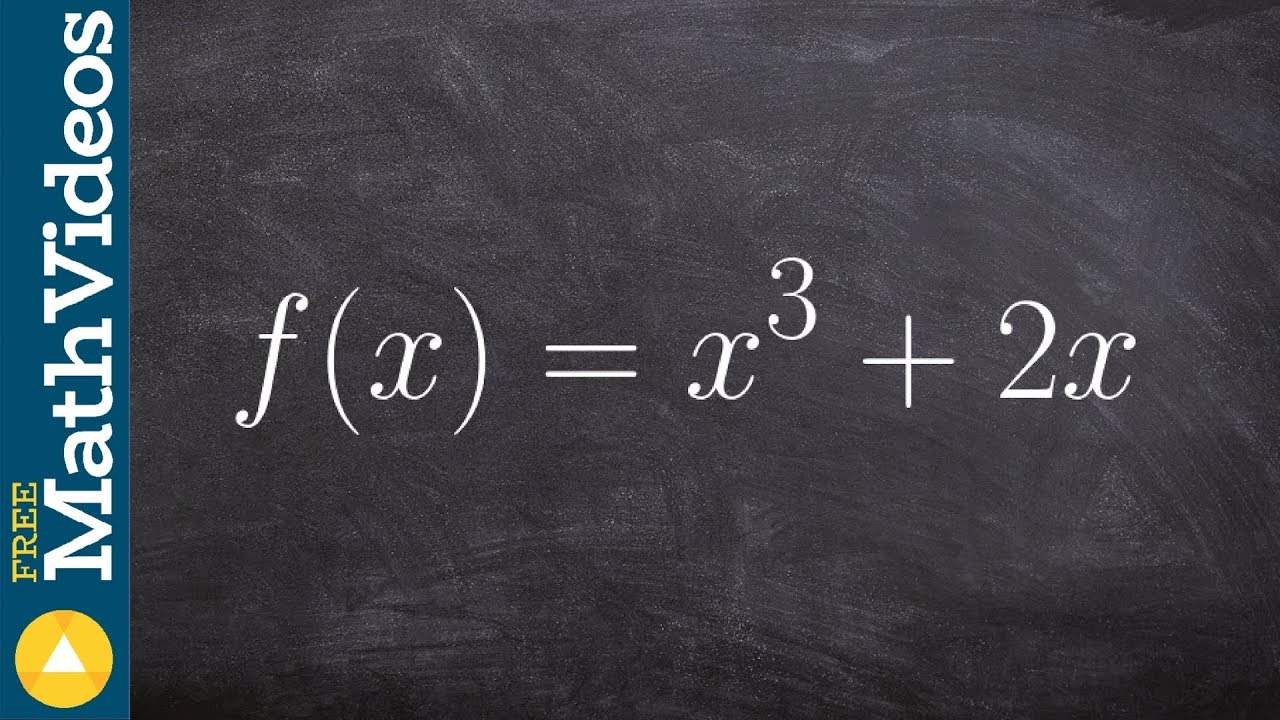Introduction and Statement of the Fundamental Theorem of Algebra

Introduction

Introduction:

The fundamental theorem of algebra is a fundamental result in the field of mathematics that relates to the properties of algebraic equations. It provides insights into the solutions of polynomial equations and is a key concept in algebraic reasoning.

Fundamental Theorem of Algebra:

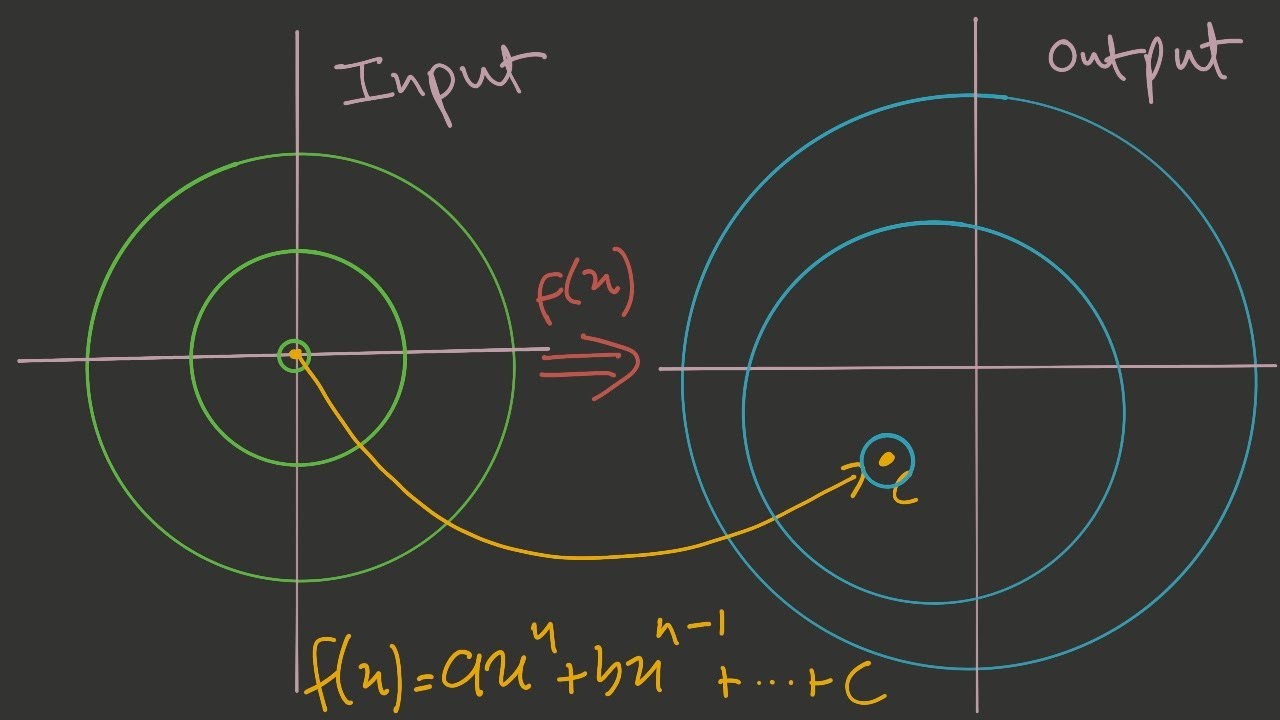
The fundamental theorem of algebra states that every non-constant polynomial equation with complex coefficients has at least one complex solution. In other words, for any polynomial equation of the form P(z) = 0, where P(z) is a polynomial with complex coefficients and z is a variable, there exists at least one complex number z0 such that P(z0) = 0.

This theorem essentially implies that every polynomial equation can be factored into linear factors, where each factor corresponds to a solution. For example, a quadratic equation like x^2 – 5x + 6 = 0 can be factored as (x – 2)(x – 3) = 0, indicating that it has two solutions, x = 2 and x = 3.

The fundamental theorem of algebra has significant implications in various areas of mathematics and science. It is not only useful in solving polynomial equations but also plays a crucial role in fields such as complex analysis, algebraic geometry, and the study of differential equations. It provides a foundational understanding of the structure and behavior of algebraic equations and is considered one of the fundamental results in mathematics.

Statement of the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra states that every non-constant polynomial equation with complex coefficients has at least one complex root. In other words, any polynomial of degree greater than or equal to 1 can be factored completely into linear factors, where each factor represents a root of the equation. This theorem is fundamental in the field of algebra as it guarantees the existence of roots for polynomial equations and allows for the solving of such equations.

Proof of the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra states that every non-constant polynomial equation with complex coefficients has at least one complex root. This means that every polynomial equation of the form:

P(z) = a₀ + a₁z + a₂z² + … + aₙzⁿ = 0

where a₀, a₁, …, aₙ are complex coefficients and z is a complex variable, has at least one solution in the complex number system.

To prove this theorem, we need to first establish two key facts:

1. Complex numbers form a complete field: This means that the complex number system is algebraically closed, which implies that every polynomial equation with complex coefficients has at least one complex root.

2. The Fundamental Theorem of Algebra holds for polynomials with real coefficients: This can be proven using techniques from algebraic and real analysis, such as the intermediate value theorem.

Once these two facts are established, we can prove the Fundamental Theorem of Algebra by considering a polynomial equation with complex coefficients.

Let’s assume we have a polynomial equation P(z) = a₀ + a₁z + a₂z² + … + aₙzⁿ = 0, where a₀, a₁, …, aₙ are complex coefficients.

First, we divide the equation by aₙ to normalize the leading coefficient:

P₁(z) = zⁿ + c₁zⁿ⁻¹ + c₂zⁿ⁻² + … + cₙ₋₁z + cₙ = 0,

where c₁ = a₁/aₙ, c₂ = a₂/aₙ, …, cₙ₋₁ = aₙ₋₁/aₙ, and cₙ = a₀/aₙ are complex constants.

Now, let’s assume that the equation P₁(z) = 0 has no complex roots, i.e., it has no solutions in the complex plane. This implies that the polynomial function P₁(z) is non-zero for all complex values of z.

We can then define a new function f(z) = 1/P₁(z). Since P₁(z) is non-zero for all complex z, f(z) is well-defined and continuous for all complex values of z.

Next, we consider the behavior of f(z) as |z| tends to infinity. Since all the coefficients c₁, c₂, …, cₙ of the polynomial P₁(z) are complex constants, we can consider the limit of f(z) as |z| → ∞.

For large values of |z|, the dominant term in the polynomial P₁(z) is the leading term zⁿ. Therefore, as |z| → ∞, the polynomial becomes dominated by the term zⁿ, and P₁(z) → zⁿ.

Thus, in the limit as |z| → ∞, f(z) → 1/zⁿ.

Now, using the fact that complex numbers form a complete field, we can apply the fundamental theorem of algebra for polynomials with real coefficients to the function f(z). Since f(z) → 1/zⁿ as |z| → ∞, we can conclude that f(z) has at least one complex root, and hence P₁(z) = 0 has at least one complex root.

This contradicts our assumption that P₁(z) = 0 has no complex roots. Therefore, the assumption must be false, and the original polynomial equation P(z) = 0 must have at least one complex root.

Hence, the Fundamental Theorem of Algebra is proven.

Applications of the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra is a fundamental result in mathematics that states that every non-constant polynomial equation with complex coefficients has at least one complex root. This theorem has various applications in different fields of mathematics and beyond. Some of the main applications of the Fundamental Theorem of Algebra include:

1. Root finding: The theorem guarantees the existence of at least one root for any polynomial equation. This is crucial in various fields, such as numerical analysis and engineering, where finding solutions to equations is essential. The theorem provides a theoretical basis for methods like Newton’s method or the bisection method, which are used to find approximate solutions to polynomial equations.

2. System of equations: The Fundamental Theorem of Algebra can be applied to systems of polynomial equations. In particular, it guarantees that the system has at least one complex solution, which can be useful in solving problems involving multiple unknowns or variables.

3. Factorization: The theorem implies that any polynomial of degree greater than or equal to 1 can be factored into linear and irreducible quadratic factors with complex coefficients. This factorization is often used in algebraic manipulations and in solving equations and systems of equations.

4. Algebraic geometry: The Fundamental Theorem of Algebra plays a fundamental role in algebraic geometry, which studies the properties and solutions of algebraic equations. It allows for the study of complex curves and surfaces and helps in understanding their structure, singularities, and intersections.

5. Real-world applications: While the theorem guarantees the existence of complex roots, it also has implications in real-world applications. For example, it is used in physics calculations involving oscillations, signal processing, and control systems. It can help determine stability and find solutions to equations arising in these areas.

6. Complex analysis: The theorem is also foundational in complex analysis, a branch of mathematics that studies functions of complex variables. It provides a basis for important concepts like analytic functions, which can be expressed as power series and have nice properties.

Overall, the Fundamental Theorem of Algebra has widespread applications in various areas of mathematics and its applications extend to numerous real-world problems. Its guarantee of the existence of complex roots allows for the development of powerful tools and methods for solving equations, studying algebraic structures, and understanding complex functions and curves.

Historical significance of the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra is a fundamental result in mathematics that states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. It is of historical significance for several reasons:

1. Validation of complex numbers: The Fundamental Theorem of Algebra provides a rigorous mathematical proof for the existence of complex numbers. Before the theorem was proven, complex numbers were viewed with skepticism and considered as “imaginary” or non-existent. The theorem showed that complex numbers are a necessary component to solve polynomial equations.

2. Resolution of longstanding mathematical problems: The theorem resolved many long-standing mathematical problems related to the roots and solutions of polynomial equations. It provided a definitive answer to questions such as whether polynomial equations of higher degree can always be completely factored or whether the solutions are finite.

3. Connection between algebra and geometry: The Fundamental Theorem of Algebra bridges the gap between algebra and geometry. It shows that the roots of polynomial equations have a geometrical interpretation as points in the complex plane. This connection between algebraic equations and geometric shapes has had profound implications in the fields of algebraic geometry and complex analysis.

4. Influence on other branches of mathematics: The theorem has had a significant impact on numerous branches of mathematics. It is a cornerstone result in complex analysis, which plays a crucial role in many areas, including physics, engineering, and computer science. The theorem also has implications in number theory, algebraic geometry, and even theoretical physics.

5. Contributions to the understanding of mathematical foundations: The proof of the Fundamental Theorem of Algebra required the development of new mathematical tools and techniques. It inspired advancements in areas such as complex analysis, topology, and abstract algebra. These advances have contributed to the overall understanding of mathematical foundations and led to the development of new branches of mathematics.

Overall, the Fundamental Theorem of Algebra has had a profound impact on mathematics, validating the existence of complex numbers, resolving long-standing problems, connecting algebra and geometry, influencing other branches of mathematics, and contributing to the understanding of mathematical foundations. It stands as one of the most important and significant theorems in the history of mathematics.

Topics related to Fundamental theorem of algebra