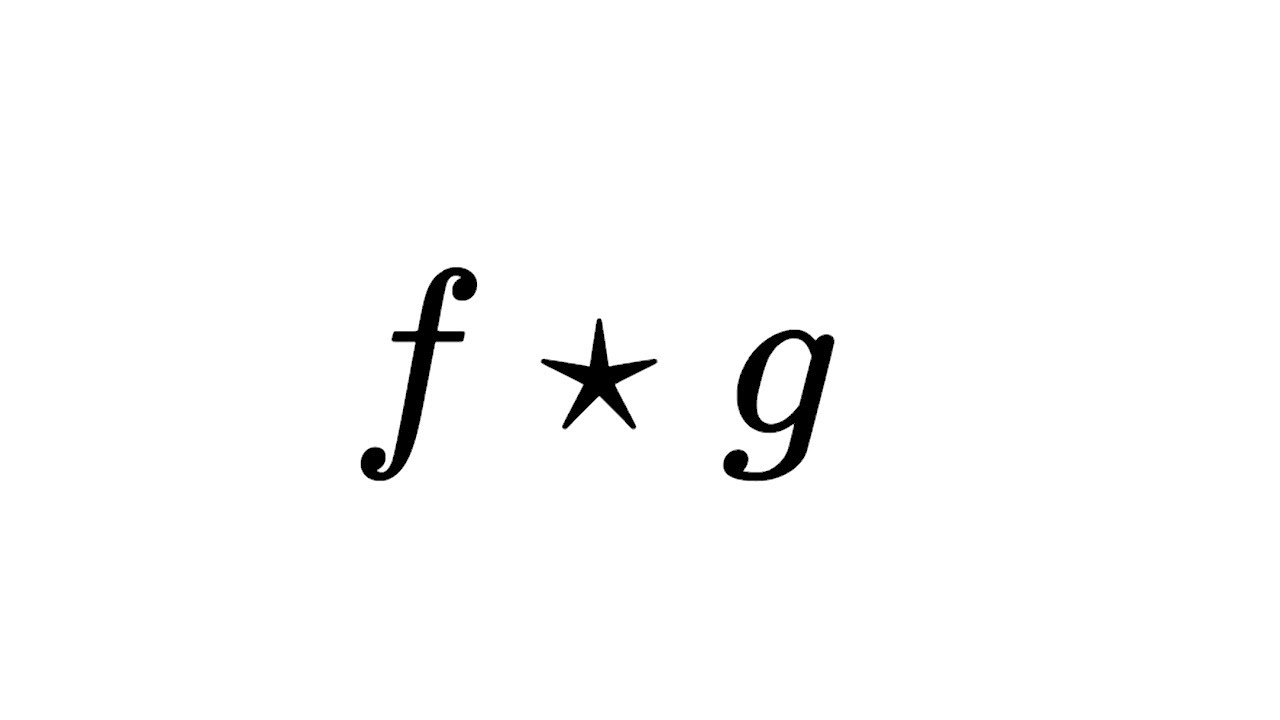Introduction to Convolution and Definition and Properties of Convolution

Introduction to Convolution

Convolution is a mathematical operation that is commonly used in signal processing and image processing. It is a mathematical operation that combines two functions or signals to create a third function or signal. It involves a process of integrating the product of two functions as one function slides over the other.

In the context of signal processing, convolution is used to describe the way that a signal is modified or transformed by another signal. It is often used to perform operations such as filtering, smoothing, and blurring on signals or images.

The basic concept of convolution involves taking two functions, usually represented as mathematical equations or graphs, and combining them to create a new function. This is done by multiplying corresponding values of the two functions together and then summing them up.

Convolution can be understood visually as sliding one function (often referred to as the kernel or the mask) over another function (often referred to as the input or the image). The kernel is usually a small function or matrix that is applied repeatedly to different regions of the input, producing the output as a result.

Convolution plays a crucial role in various fields, including digital signal processing for audio and video signals, image processing for edge detection, feature extraction, and image enhancement, and also in deep learning and neural networks, where convolutional layers are used for object recognition and image classification.

Overall, convolution is a fundamental operation in the field of signal and image processing, as well as other areas of mathematics and computer science, and it allows us to analyze, transform, and manipulate data in various ways.

Definition and Properties of Convolution

In mathematics and signal processing, convolution is an operation that combines two functions or signals to produce a third function or signal. It is represented mathematically using the symbol “*”. The resulting function is typically dependent on the overlapping of the two input functions.

Formally, given two functions f and g defined as f(t) and g(t), the convolution operation is defined as:

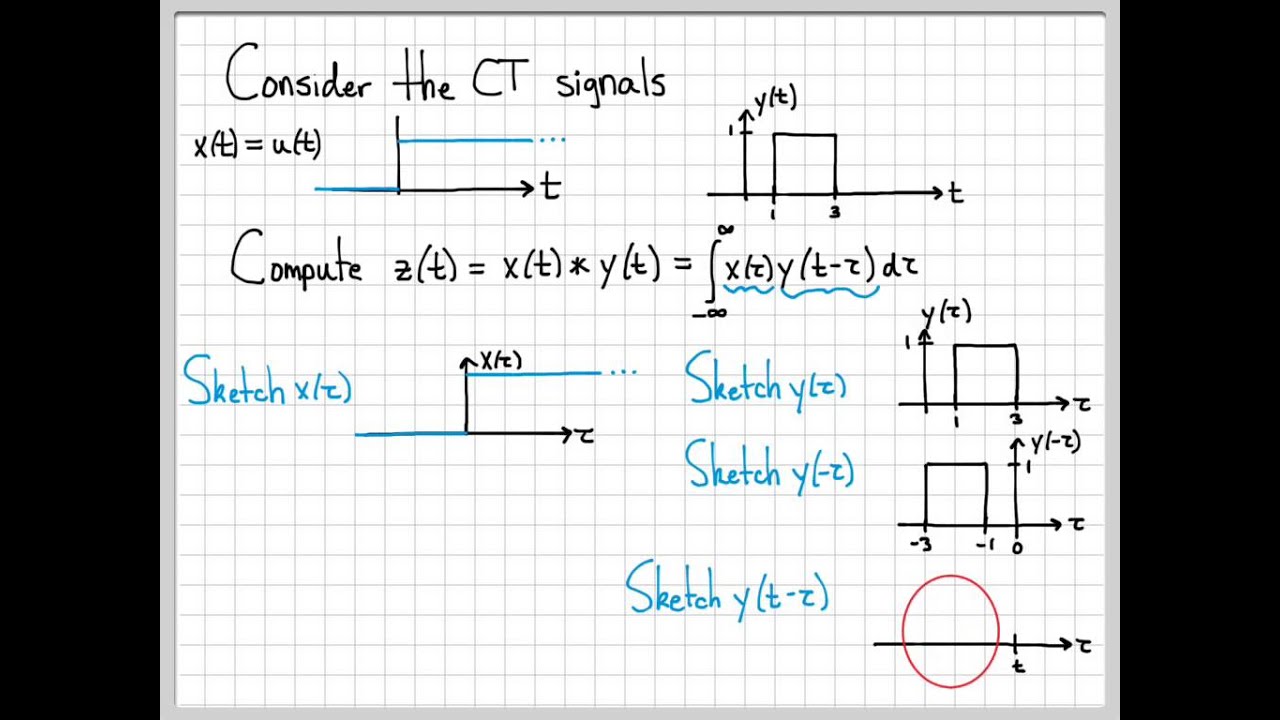
f * g(t) = ∫(from -∞ to +∞) f(tau) * g(t-tau) d(tau)

Here, “*” denotes convolution, and t is the variable of the resulting function. The integral represents the weighted sum of products between the values of f and g, with g being shifted by tau.

Properties of convolution include:

1. Commutativity: The order of the functions can be reversed without affecting the result, i.e., f * g = g * f.

2. Associativity: Convolution is associative, meaning that (f * g) * h = f * (g * h).

3. Distributivity: Convolution distributes over addition, i.e., f * (g + h) = f * g + f * h.

4. Linearity: Convolution is a linear operation, meaning that c1 * (f * g) + c2 * (h * g) = (c1 * f + c2 * h) * g, where c1 and c2 are constants.

5. Convolution with the Dirac delta function: Convolution of a function f(t) with the Dirac delta function δ(t) results in the function itself, i.e., f * δ(t) = f(t).

Convolution is extensively used in various fields, including image and signal processing, probability theory, and physics, aiding in the analysis and manipulation of data.

Convolution in Signal Processing

Convolution is a fundamental operation in signal processing that combines two signals to create a third signal. It involves multiplying the amplitudes of corresponding samples of two signals and summing them up.

In signal processing, signals are typically represented as discrete sequences of values. The process of convolution involves shifting one of the signals and multiplying each value of that signal with the corresponding value of the other signal. The products are then added together to obtain a new sequence, which forms the convolved signal.

Mathematically, the convolution of two discrete signals x[n] and h[n] is denoted as y[n] and is calculated by the following formula:

y[n] = ∑ x[k] * h[n – k]

Here, k represents the index of the summation and determines the alignment of the two signals. The convolution operation is often denoted by the symbol “*”.

Convolution has several important applications in signal processing. It is commonly used in systems analysis, filtering, and modeling. For example, in digital filtering, convolution is used to apply filter coefficients to an input signal. It is also utilized in image processing, where it can be used for tasks such as blurring, edge detection, and image reconstruction.

In summary, convolution is a key operation in signal processing that combines two signals by multiplying corresponding samples and summing them up. It has wide-ranging applications and is crucial in various areas of signal analysis and processing.

Applications of Convolution in Mathematics

Convolution is a mathematical operation that combines two functions to produce a third function that represents the amount of overlap between the original functions. It finds applications in various areas of mathematics, including:

1. Signal Processing: Convolution is widely used in signal processing to analyze and manipulate signals. It allows for operations such as filtering, smoothing, and noise reduction. For example, it can be used to convolve a signal with a filter to extract certain frequencies or to convolve a noisy signal with a smoothing kernel to reduce noise.

2. Probability Theory: In probability theory, convolution plays a crucial role in the study of the sum of random variables. Given two random variables, their convolution gives the probability distribution of the sum of these variables. This concept is used to analyze various probabilistic systems, such as queues, networks, and complex models with many interacting elements.

3. Image Processing: Convolution is extensively used in image processing for tasks such as image filtering, edge detection, and image enhancement. By convolving an image with a specific kernel or filter, different features or characteristics can be extracted or enhanced. Moreover, convolutional neural networks (CNNs) have revolutionized the field of computer vision by utilizing convolutional layers to learn features from images.

4. Differential Equations: Convolution finds applications in solving differential equations. Specifically, in solving linear constant coefficient ordinary differential equations (ODEs), convolution is used to obtain the solution through the convolution theorem. This allows for a more streamlined and efficient method of solving differential equations.

5. Fourier Analysis: In Fourier analysis, convolution is used to relate the Fourier transforms of two functions. The convolution theorem states that the Fourier transform of the convolution of two functions is equal to the pointwise product of their respective Fourier transforms. This property is utilized to solve problems involving Fourier series, Fourier transforms, and frequency analysis.

6. Numerical Analysis: Convolution is employed in numerical analysis for tasks such as interpolation and approximation. For example, the discrete convolution can be used to interpolate missing data points or to approximate one function by convolving it with an appropriate kernel function.

Overall, convolution is a powerful mathematical operation that finds applications in diverse fields such as signal processing, probability theory, image processing, differential equations, Fourier analysis, and numerical analysis. Its ability to capture the interaction between functions makes it a valuable tool in solving many real-world problems.

Conclusion

In conclusion, convolution is a mathematical operation that combines two functions to produce a third function. It is commonly used in signal processing and image recognition tasks to extract useful features and gather information from the input data. Convolution has proven to be a powerful tool in various areas of science and engineering, contributing to advancements in fields such as computer vision, speech recognition, and deep learning. Its ability to capture local patterns and correlations has made it an essential technique in many applications. Overall, convolution plays a crucial role in extracting meaningful information from data and is a fundamental concept in many areas of research and technology.

Topics related to Convolution