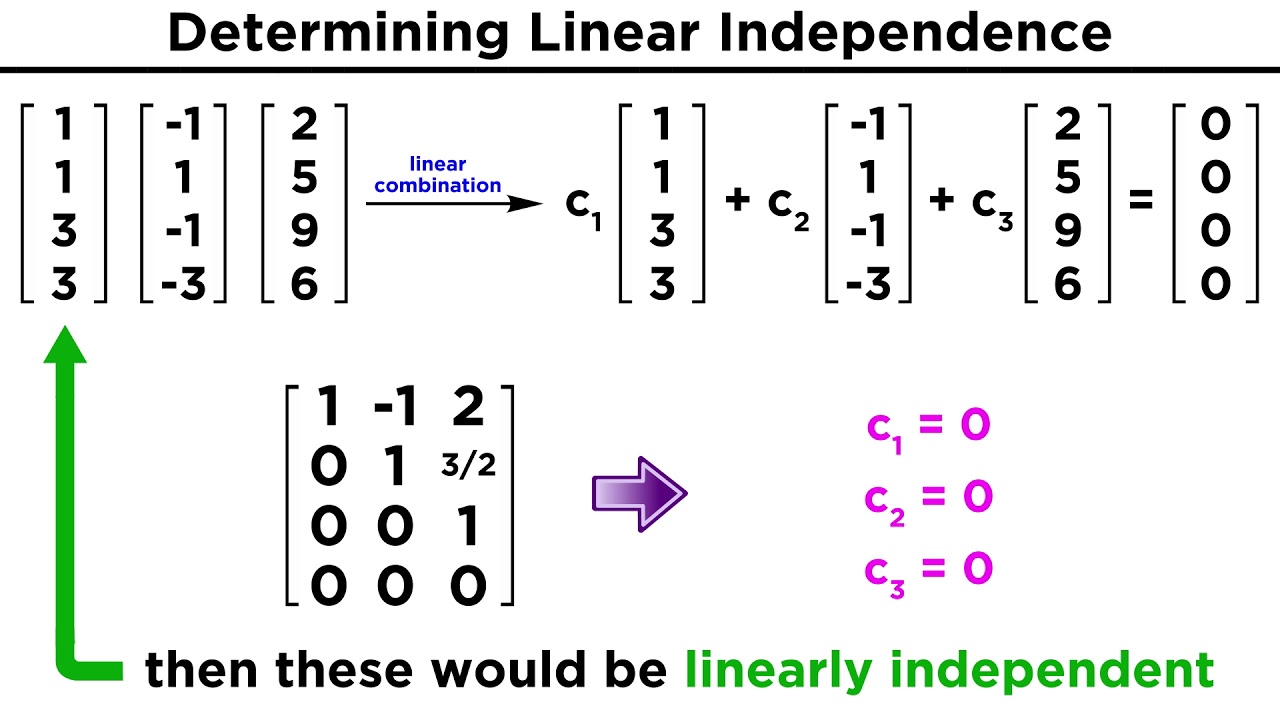
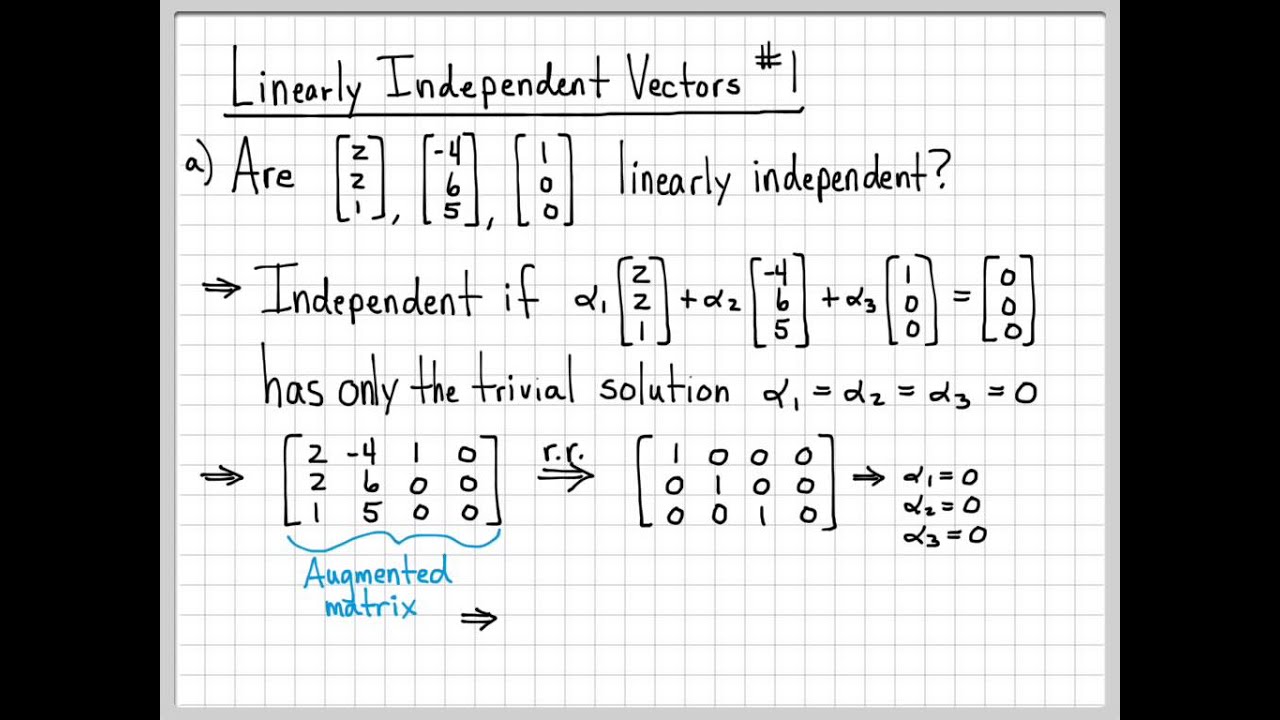
Definition of linear independence and Testing for linear independence

Definition of linear independence

Linear independence is a concept in linear algebra that refers to a set of vectors in a vector space. If a set of vectors is linearly independent, it means that none of the vectors in the set can be expressed as a linear combination of the other vectors in the set.

In other words, if vectors v1, v2, …, vn are linearly independent, then no vector in the set can be written as a linear combination of the others. This implies that any non-zero coefficient assignment for the vector equation c1v1 + c2v2 + … + cnvn = 0 must have c1 = c2 = … = cn = 0, for the equation to hold true.

Linear independence is an important concept because it helps determine the span, dimension, and basis of a vector space. It is also a key property for solving systems of linear equations and performing various operations in linear algebra.

Testing for linear independence

Testing for linear independence is a mathematical process used to determine if a set of vectors is linearly independent.

A set of vectors is linearly independent if none of the vectors in the set can be expressed as a linear combination of the others. In other words, no vector in the set can be written as a sum of scalar multiples of the other vectors.

To test for linear independence, we can set up a system of equations using the vectors in the set. Let’s say we have a set of vectors v1, v2, …, vn.

We can write the linear combinations as follows:

a1 * v1 + a2 * v2 + … + an * vn = 0

where a1, a2, …, an are scalar coefficients and the zero vector is the result of the linear combination.

If the only solution to this system of equations is the trivial solution (a1 = a2 = … = an = 0), then the set of vectors is linearly independent. This means that no vector in the set can be expressed as a linear combination of the others.

If the system of equations has a non-trivial solution (non-zero coefficients), then the set of vectors is linearly dependent. This means that at least one vector in the set can be written as a linear combination of the others.

In summary, to test for linear independence, we set up and solve a system of equations using the vectors in the set. If the only solution is the trivial solution, the vectors are linearly independent. Otherwise, they are linearly dependent.

Properties of linearly independent vectors

Linearly independent vectors are vectors that cannot be represented as a linear combination of other vectors in a vector space.

Here are some properties of linearly independent vectors:

1. Definition: A set of vectors {v1, v2, …, vn} is linearly independent if the only solution to the equation a1v1 + a2v2 + … + anvn = 0, where a1…an are scalars, is a1 = a2 = … = an = 0. In other words, the only way for the sum of the vectors to equal the zero vector is if all the coefficients are zero.

2. No redundancy: Linearly independent vectors provide unique information. Each vector in a linearly independent set contributes something new to the linear combination, and removing any vector from the set would decrease its dimensionality.

3. Spanning property: Linearly independent vectors can span an entire vector space. If a set of vectors is linearly independent and has the same dimension as the vector space, then it is said to be a basis for that vector space. Any vector in the vector space can be uniquely expressed as a linear combination of the basis vectors.

4. Dimensionality: The maximum number of linearly independent vectors in a vector space is equal to its dimension. If a vector space has a dimension of n, it can have at most n linearly independent vectors.

5. Orthogonality: Orthogonal vectors (vectors that are perpendicular to each other) are always linearly independent. This is because their dot product is zero, leading to a unique solution when trying to write one vector as a linear combination of the other.

6. Linear dependence: If a set of vectors is not linearly independent, it is said to be linearly dependent. This means that at least one vector in the set can be expressed as a linear combination of the remaining vectors.

Linear dependence and linear independence in equations

In mathematics, linear dependence and linear independence refer to the relationships between vectors or equations in a vector space.

When a set of vectors is linearly dependent, it means that at least one vector in the set can be written as a linear combination of the others. In other words, there exists a nontrivial solution to a linear equation involving the vectors. For example, if we have vectors v1, v2, and v3, and we can express v3 as a combination of v1 and v2, say v3 = 2v1 + 3v2, then the set of vectors {v1, v2, v3} is linearly dependent.

On the other hand, if a set of vectors is linearly independent, it means that no vector in the set can be written as a linear combination of the others, except for the trivial case when all coefficients are zero. In other words, all the vectors in the set are distinct and not redundant. For example, if we have vectors u1, u2, and u3, and there are no nonzero coefficients that satisfy the equation u3 = a*u1 + b*u2, except when a = 0 and b = 0, then the set of vectors {u1, u2, u3} is linearly independent.

Linear independence is a desirable property in many mathematical and engineering applications because it signifies that the vectors or equations provide unique and non-redundant information. It allows us to solve systems of linear equations and perform calculations with more efficiency and accuracy.

Applications of linear independence in math and beyond

Linear independence is a fundamental concept in mathematics with various applications in different areas. Here are some examples of its applications:

1. Linear Algebra: Linear independence is crucial in solving systems of linear equations. A set of vectors is linearly independent if none of them can be written as a linear combination of the others. The concept is used to determine whether a system has a unique solution or not, and to find basis and dimension of vector spaces.

2. Matrix Theory: In matrix theory, linear independence is key to understanding the rank of a matrix. The rank is the maximum number of linearly independent columns or rows in a matrix, and it provides information on the properties and solutions of systems of linear equations.

3. Change of Basis: Linear independence is used in change of basis in vector spaces. Given two bases of a vector space, linear independence is required to represent vectors uniquely in terms of the new basis.

4. Linear Differential Equations: Linear independence of solutions of homogeneous linear differential equations is essential in finding the general solution. If a set of solutions is linearly independent, then any linear combination of those solutions will also be a solution to the differential equation.

5. Linear Programming: In optimization problems, linear independence helps determine the feasibility of a solution. In linear programming, constraints are typically represented as linear equations or inequalities, and linear independence is used to ensure that the set of constraints is not redundant or contradictory.

6. Signal Processing: Linear independence is employed in analyzing and processing signals. It helps in expressing signals in terms of a set of basis functions or analyzing the linear combination of different signals.

7. Control Systems: In control theory, linear independence is used to analyze and design feedback control systems. It is crucial in determining controllability and observability of systems, which are essential properties for achieving desired system behavior.

8. Quantum Mechanics: In quantum mechanics, the concept of linear independence is fundamental in describing the state of a quantum system. The wavefunctions representing the possible states of a system must be linearly independent to ensure a unique and meaningful description.

9. Machine Learning: Linear independence can be employed in machine learning algorithms. For example, in feature selection, linear independence can help identify the most informative and non-redundant features for a particular task.

10. Computer Graphics: Linear independence plays a role in computer graphics, particularly in rasterization and rendering algorithms. It helps in determining the visibility of objects and the calculation of lighting and shading effects.

Overall, linear independence is a crucial concept that finds applications in numerous areas of mathematics and beyond, serving as a foundation for solving problems and understanding various phenomena.

Topics related to Linear independence