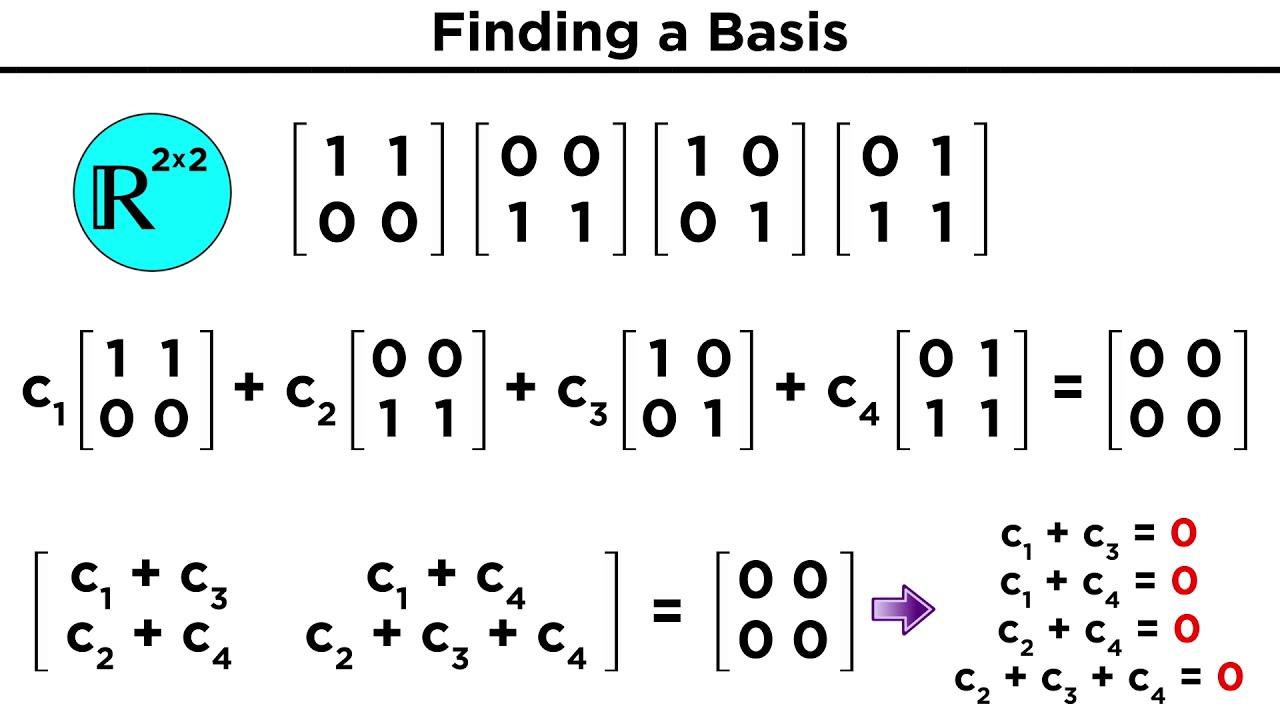
Definition of Basis in Mathematics and Basis in Linear Algebra

Definition of Basis in Mathematics

In mathematics, a basis refers to a set of vectors that can be used to represent and span a vector space.

More formally, a basis for a vector space V is a set of vectors {v1, v2, …, vn} that satisfy two conditions:

1. Linear independence: The vectors in the basis set are linearly independent, meaning that no vector in the set can be expressed as a linear combination of the others. This implies that none of the vectors in the basis set can be written as a scalar multiple of any other vector in the set.

2. Spanning set: Every vector in the vector space V can be expressed as a unique linear combination of the vectors in the basis set. In other words, the basis set spans the entire vector space.

The dimension of a vector space is the number of vectors in any basis set for that space.

Bases are important in linear algebra, as they provide a convenient way to represent vectors and perform calculations. They allow us to express any vector in the vector space using a unique combination of the basis vectors.

Basis in Linear Algebra

In linear algebra, a basis is a set of vectors that span a particular vector space and are linearly independent.

To understand this concept, first, let’s define what it means for vectors to span a vector space. Given a vector space V, a set of vectors {v1, v2, …, vn} spans V if any vector in V can be written as a linear combination of these vectors. In other words, for any vector v in V, there exist scalars c1, c2, …, cn such that v = c1v1 + c2v2 + … + cnvn.

Next, we can define linear independence. A set of vectors {v1, v2, …, vn} is said to be linearly independent if the only solution to the equation c1v1 + c2v2 + … + cnvn = 0 is c1 = c2 = … = cn = 0. In other words, there are no non-trivial linear combinations of these vectors that equal the zero vector.

Given these definitions, a basis in linear algebra is a set of vectors that satisfies two conditions: spanning the vector space, and being linearly independent. In simpler terms, a basis is a minimal set of vectors that can express every vector in the vector space, and no vector in the basis can be expressed as a linear combination of the others.

Bases are essential as they provide a way to represent vectors as a unique combination of basis vectors. This allows us to simplify computations and understand the structure of vector spaces. Additionally, bases serve as a foundation for many other concepts in linear algebra, such as dimension, coordinates, and transformations.

Basis in Abstract Algebra

In abstract algebra, a basis refers to a set of elements that are linearly independent and can be used to generate all other elements of a given algebraic structure.

More specifically, in a vector space, a basis is a set of vectors that spans the entire vector space, meaning that every vector in the space can be expressed as a linear combination of the basis vectors. Additionally, a basis must be linearly independent, which means that no vector in the basis can be written as a linear combination of the other vectors in the basis.

For example, in the vector space of 2-dimensional vectors (R^2), the set {(1,0), (0,1)} forms a basis. Any vector in R^2 can be represented as a linear combination of these basis vectors. For instance, the vector (2,3) can be expressed as 2(1,0) + 3(0,1).

In abstract algebra, other algebraic structures such as groups, rings, and modules may also have bases. In these cases, the basis elements are used to generate the other elements of the structure. However, the notion of linear independence does not always apply as it does in vector spaces.

Overall, the concept of a basis is crucial in abstract algebra as it provides a way to understand and characterize the structure and properties of various algebraic systems.

Basis in Topology

In topology, a basis is a collection of sets that allows us to define a topology on a given set. A basis consists of sets called basis elements, and the topology generated by the basis is the collection of all possible unions of these basis elements.

More formally, a basis for a topology on a set X is a collection B of subsets of X such that every open set in the topology can be expressed as a union of basis elements. This means that for any open set U, there exists a collection of basis elements {B_i} such that U is the union of all the B_i’s.

Bases are useful because they allow us to characterize topological spaces in terms of simpler structures. For example, in a metric space, a basis can be defined using open balls centered at each point. In this case, the topology generated by the basis is the same as the metric topology defined by the distance function.

Bases also help us to understand and compare different topologies. If two topologies share the same basis, they have the same collection of open sets, and therefore are equivalent. On the other hand, if one topology has a basis that is finer (i.e., contains more open sets) than the other, then the finer topology is said to be stronger or more refined.

Overall, bases provide a way to construct and study topologies on sets, and they are an important concept in the field of topology.

Basis in Functional Analysis

In functional analysis, a basis is a fundamental concept used to describe the structure of a vector space. A basis is a set of vectors that can be used to express any vector in the vector space as a linear combination of these basis vectors. Specifically, if we have a vector space V, a basis B is a set of linearly independent vectors in V, such that any vector in V can be written as a unique linear combination of the basis vectors.

Formally, let V be a vector space over a field F. A subset B = {v1, v2, …, vn} of V is called a basis for V if the following conditions hold:

1. Linear independence: The vectors in B are linearly independent, meaning that no non-trivial linear combination of the basis vectors equals the zero vector. This can be expressed as the condition that the equation c1v1 + c2v2 + … + cnvn = 0, where ci are scalars, has only the trivial solution c1 = c2 = … = cn = 0.

2. Spanning set: Every vector in V can be expressed as a linear combination of the basis vectors. This means that for any vector v in V, there exist scalars c1, c2, …, cn such that v = c1v1 + c2v2 + … + cnvn.

3. Linear independence as linear combinations: The basis vectors v1, v2, …, vn cannot be expressed as linear combinations of each other. In other words, there is no non-trivial equation of the form ci1v1 + ci2v2 + … + cinvn = 0, where not all the ci are zero scalars.

By having a basis, one can represent any vector in the vector space using the coefficients of the linear combination of the basis vectors. This allows for a convenient way to study the properties and transformations of vectors in functional analysis.

Topics related to Basis