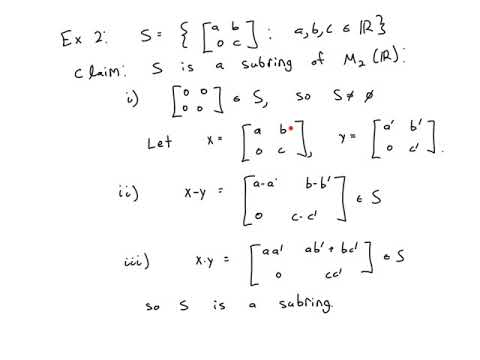Definition of Subring and Properties and Examples of Subrings

Definition of Subring

A subring is a subset of a given ring that is itself a ring with respect to the same ring operations. In other words, a subring of a ring R is a subset S of R such that S is closed under addition, multiplication, and additive inverses, and forms a ring under these operations. Note that a subring may include the multiplicative identity of the original ring or not.

Properties and Examples of Subrings

A subring of a ring is a subset of the ring that is itself a ring under the same operations as the original ring. In other words, it is a subset that is closed under addition, subtraction, and multiplication, and contains the additive identity element and is closed under additive inverses.

Here are some properties and examples of subrings:

1. Subrings have the same addition and multiplication operations as the original ring. This means that if R is a ring and S is a subring of R, then the addition operation in S is the same as the addition operation in R, and similarly for multiplication.

2. Subrings contain the same additive identity element as the original ring. This means that the zero element of S is the same as the zero element of R.

3. Subrings are closed under addition, subtraction, and multiplication. This means that if a and b are elements of S, then a + b and a – b are also elements of S, and if a and b are elements of S, then a * b is also an element of S.

4. Subrings contain additive inverses. This means that for every element a in S, the additive inverse of a, denoted as -a, is also an element of S.

Examples of subrings:

1. The subring of integers (Z) contained within the real numbers (R). Z is closed under addition, subtraction, and multiplication, and contains the additive identity element 0 and additive inverses for every element.

2. The subring of even integers (2Z) contained within the integers (Z). 2Z is closed under addition, subtraction, and multiplication, and contains the additive identity element 0 and additive inverses for every element.

3. The subring of 2×2 matrices with integer entries contained within the set of all 2×2 matrices with real entries. This subring is closed under matrix addition, subtraction, and multiplication, and contains the zero matrix as the additive identity element and additive inverses for every matrix.

Subring vs Subfield

In mathematics, a subring refers to a subset of a ring that is itself a ring with respect to the same addition and multiplication operations as the original ring. This means that it must be closed under addition, subtraction, and multiplication, and it must also contain the additive identity and multiplicative identity elements.

On the other hand, a subfield is a subset of a field that is itself a field, again with respect to the same addition and multiplication operations as the original field. In addition to the requirements of closure under addition, subtraction, and multiplication, a subfield must also be closed under division (except by zero), and contain the additive and multiplicative identity elements.

In summary, the main difference between a subring and a subfield is related to the additional requirement of division for subfields. While both subrings and subfields are subsets of a larger algebraic structure that are closed under the relevant operations, subfields have the added property of being closed under division, which sets them apart from subrings.

Subring Criteria and Testing

A subring is a subset of a given ring that is itself a ring under the same operations. In other words, it is a smaller ring contained within a larger ring. To determine if a subset is a subring, we need to check for the following criteria:

1. Closure under addition and multiplication: A subset S of a ring R is a subring if it is closed under addition and multiplication. This means that for any elements a, b in S, the sum a + b and the product a * b are also in S.

2. Existence of additive inverse: A subring must contain the additive identity (usually denoted as 0) of the larger ring R, as well as the additive inverse of each element. This means that for any element a in S, its additive inverse -a must also be in S.

3. Closure under subtraction: A subring must be closed under subtraction. This means that for any elements a, b in S, their difference a – b must also be in S.

4. Non-empty: A non-empty subset is required for a subring. It must contain at least one element.

To test if a given subset is a subring, we can apply these criteria to the specific operations and elements involved. We need to verify that the subset satisfies all the above conditions for being a subring. If it meets all the criteria, then it can be considered a subring of the larger ring.

It’s important to note that a subring may not necessarily have the same unity element or identity element as the original ring, but it must have its own identity element which acts as the multiplicative identity for the subring.

In summary, a subring is a subset of a ring that is itself a ring. To determine if a subset is a subring, we need to ensure closure under addition and multiplication, existence of additive inverse, closure under subtraction, and non-emptiness.

Applications and Importance of Subrings

Subrings are a fundamental concept in abstract algebra that have various applications and importance. Here are some examples of their applications and importance:

1. Understanding Ring Structure: Subrings allow us to analyze the internal structure of a given ring. By identifying and studying subrings, we can gain insights into the algebraic properties and behaviors of the larger ring.

2. Construction of New Rings: Subrings provide a way to construct new rings from existing ones. By taking a subset of a ring that is closed under addition, subtraction, and multiplication, we can define a subring that inherits certain properties from the original ring. This construction allows for the creation of new rings with specific desired properties.

3. Ring Homomorphisms: Subrings play a crucial role in defining and studying ring homomorphisms. When we have two rings, a homomorphism is a map between them that preserves the algebraic structure. By considering subrings, we can investigate the existence and properties of ring homomorphisms between different rings.

4. Ideal Theory: Subrings are intimately connected to the concept of ideals in algebra. Ideals are special types of subrings that have additional properties, and they have significant importance in various areas of mathematics, such as commutative algebra and algebraic number theory. By studying subrings, we can understand the relationship between them and their corresponding ideals, which provides insight into the structure and properties of rings.

5. Algebraic Geometry: Subrings have applications in algebraic geometry, a branch of mathematics that studies the geometry of algebraic varieties. In this field, subrings often appear as coordinate rings or function rings associated with algebraic varieties. These rings carry important information about the geometric properties and structure of the underlying variety.

In conclusion, subrings have a wide range of applications and importance in abstract algebra. They help in understanding ring structure, constructing new rings, defining ring homomorphisms, exploring ideal theory, and studying algebraic varieties in algebraic geometry. Subrings are an essential tool for investigating the properties and behaviors of rings and offer valuable insights into various areas of mathematics.

Topics related to Subring