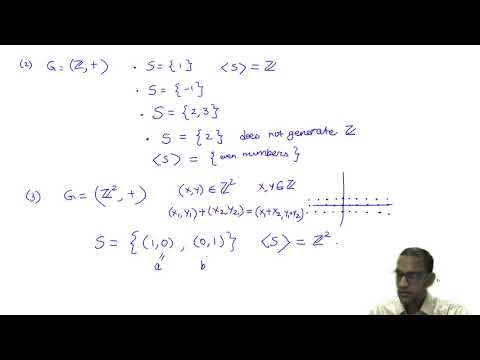Definition of a free group and Properties of free groups

Definition of a free group

A free group is a concept in group theory, which is a branch of abstract algebra. In group theory, a group is a set of elements along with a binary operation, typically denoted as multiplication, that satisfies certain properties.

A free group is a specific type of group that is generated by a set of elements, where no relations are imposed on these elements except for the necessary ones implied by the group axioms. This means that the elements in a free group can be freely combined and multiplied together, without any constraints on how they should interact.

Formally, a free group with a generating set S is denoted as F(S) or ⟨S⟩. Elements of F(S) are represented as words in the alphabet S and its inverses, i.e., the elements of S and their reciprocals. Two words are considered equal if they represent the same element in F(S), which means that they can be transformed into each other by rearranging the factors and applying inverses.

The defining property of a free group is that there are no nontrivial relations among the generators. This means that any product of elements in the generating set is distinct and can only be equal to the identity element if and only if all the factors cancel pairwise.

Free groups have numerous applications in mathematics and other fields, such as in topology, geometry, and cryptography. They play a fundamental role in understanding the structure and behavior of more general groups and provide a useful framework for studying abstract notions of symmetry and transformations.

Properties of free groups

A free group is a concept in abstract algebra that has certain properties. Here are some key properties of free groups:

1. Definition: A free group is a group that is not constrained by any relations between its elements. This means that the group is freely generated by a set of elements, which we can call generators, and there are no additional relations imposed upon these generators.

2. Generators: A free group is generated by a set of elements, usually denoted as “X.” These generators form a basis for the group, and any element of the group can be expressed as a product of these generators (and their inverses).

3. Word: In a free group, an element is represented as a “word” in the generators and their inverses. This word is a sequence of the generators and their inverses, which can be concatenated together.

4. Reduced words: A reduced word is a word where no adjacent generator and its inverse appear consecutively. In other words, there are no cancellations between a generator and its inverse. The reduced word is unique for each element in the free group.

5. Uniqueness: Every element in the free group can be expressed as a unique reduced word, meaning that different reduced words represent different elements of the group.

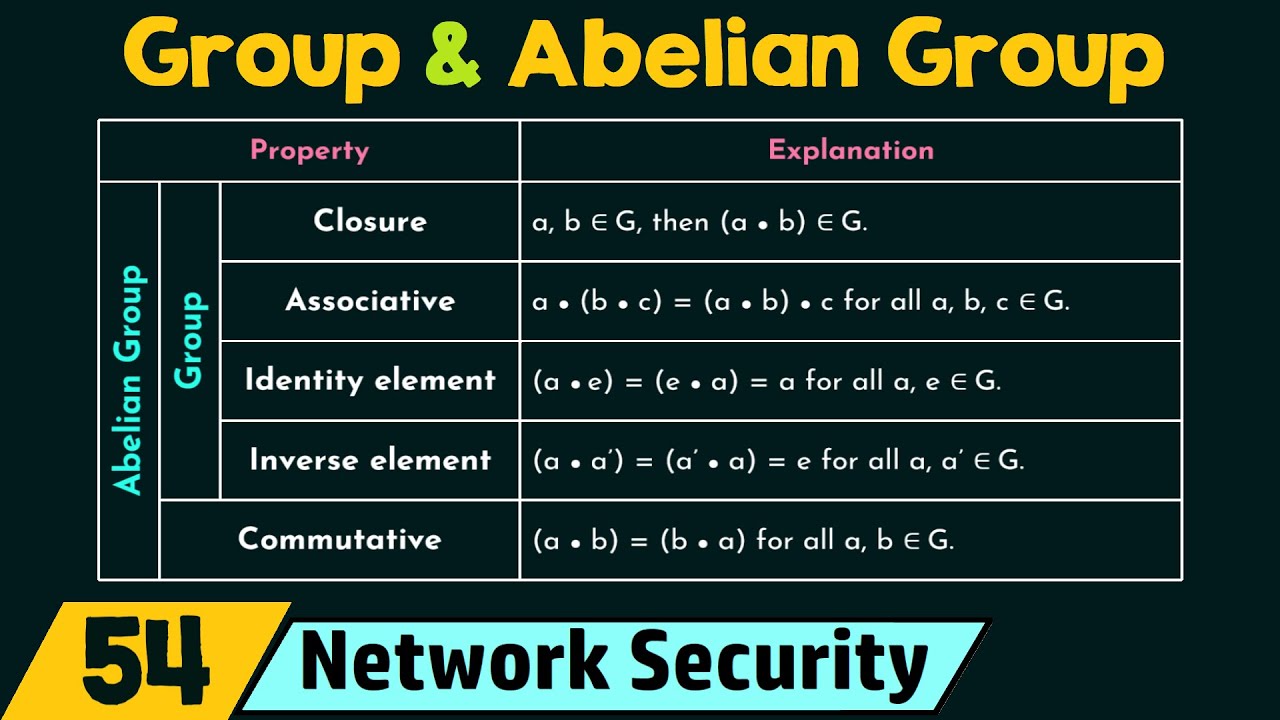
6. Group structure: Free groups have a well-defined group structure, meaning that they satisfy the group axioms of closure, associativity, identity element, and inverse elements.

7. Universal property: Free groups have a universal property, which states that any map from the generators to any group can be extended to a unique group homomorphism from the free group to that group.

8. Isomorphism: Free groups are isomorphic if and only if they have the same number of generators.

These are some of the main properties of free groups. They have various applications in mathematics, particularly in algebraic topology, group theory, and geometric group theory.

Relations and generators in free groups

In the theory of free groups, there are two fundamental concepts: relations and generators.

A free group is a group that is generated by a set of elements, called generators, with no additional relations imposed on them. For example, suppose we have two elements, a and b. The free group generated by these elements, denoted as F(a, b), consists of all possible words in a and b and their inverses. So, elements of F(a, b) would look like a, b, a^-1, b^-1, ab, ba, a^-1b, etc.

Relations, on the other hand, are equations or words involving the generators that are imposed as constraints on the group. These relations can be thought of as rules that define how the generators interact with each other. For example, suppose there is a relation given by the word ab^-1. This relation means that the product of a and b^-1 should be equal to the identity element of the group. In other words, in the group F(a, b), we have the relation ab^-1 = 1.

By adding relations to a free group, we obtain a new group called a quotient group. The quotient group is obtained by taking the free group and quotienting out by the normal subgroup generated by the relations. This means that any element that satisfies the relations is identified with the identity element in the quotient group.

Generators and relations play an important role in the study of free groups and their applications in various areas of mathematics, such as algebra, topology, and combinatorics. They provide a way to describe and analyze the structure of groups and understand their properties.

Examples of free groups

Examples of free groups include:

1. The trivial group: This is the simplest example of a free group. It consists of a single element, often denoted as the identity element or the empty word. In this group, any operation with the identity element results in itself.

2. The cyclic group: A cyclic group is a group generated by a single element, denoted as . It consists of all possible powers of a and their inverses. For example, the group generated by the element a could have elements {a, a^2, a^3, …, a^(-1), a^(-2), …}.

3. The free group on two generators: This is a more general example of a free group that is generated by two elements, often denoted as . It consists of all possible combinations of these generators and their inverses. For example, it could have elements {a, b, a^(-1), b^(-1), ab, ba, a^(-1)b, b^(-1)a, …}.

The free group concept can be extended to any number of generators, and each additional generator increases the complexity of the group.

Applications of free groups in mathematics

Free groups have several applications in different areas of mathematics. Some of the notable applications include:

1. Algebraic Topology: Free groups arise naturally as fundamental groups of certain spaces. For example, the fundamental group of a wedge sum of circles is a free group. Free groups are also used in various techniques and constructions in algebraic topology, such as covering spaces and Seifert-van Kampen theorem.

2. Geometric Group Theory: Free groups play a crucial role in the study of geometric properties of groups. The notion of a Cayley graph, which is a geometric representation of a group, is based on the generating set of a free group. Geometric group theory explores the connection between the algebraic and geometric properties of groups using free groups.

3. Combinatorics: Free groups are often used in combinatorial settings to model various mathematical structures. For example, in graph theory, free groups can be used to study graph presentations and graph genus. Free groups are also used in the study of discrete structures and combinatorial optimization problems.

4. Number Theory: Free groups are used in the study of number fields and algebraic number theory. In particular, free groups arise when studying Galois groups, which are groups associated with the solutions of polynomial equations. The theory of free groups provides a framework for the study of these groups and their properties.

5. Knot Theory: Free groups are often used in the study of knots and links. The fundamental group of the complement of a knot or link is a free group, and this fact is instrumental in understanding the topology of knots. Free groups are also used in the study of braids and their relations.

6. Group Theory: Free groups serve as building blocks in the theory of groups. Many groups can be expressed as quotients or extensions of free groups. For example, every finitely generated group can be presented as a quotient of a free group. Studying free groups helps to understand the structure and properties of more general groups.

These are just a few examples of how free groups are applied in mathematics. Free groups provide a flexible and powerful tool for understanding various mathematical structures and their interactions.

Topics related to Free group