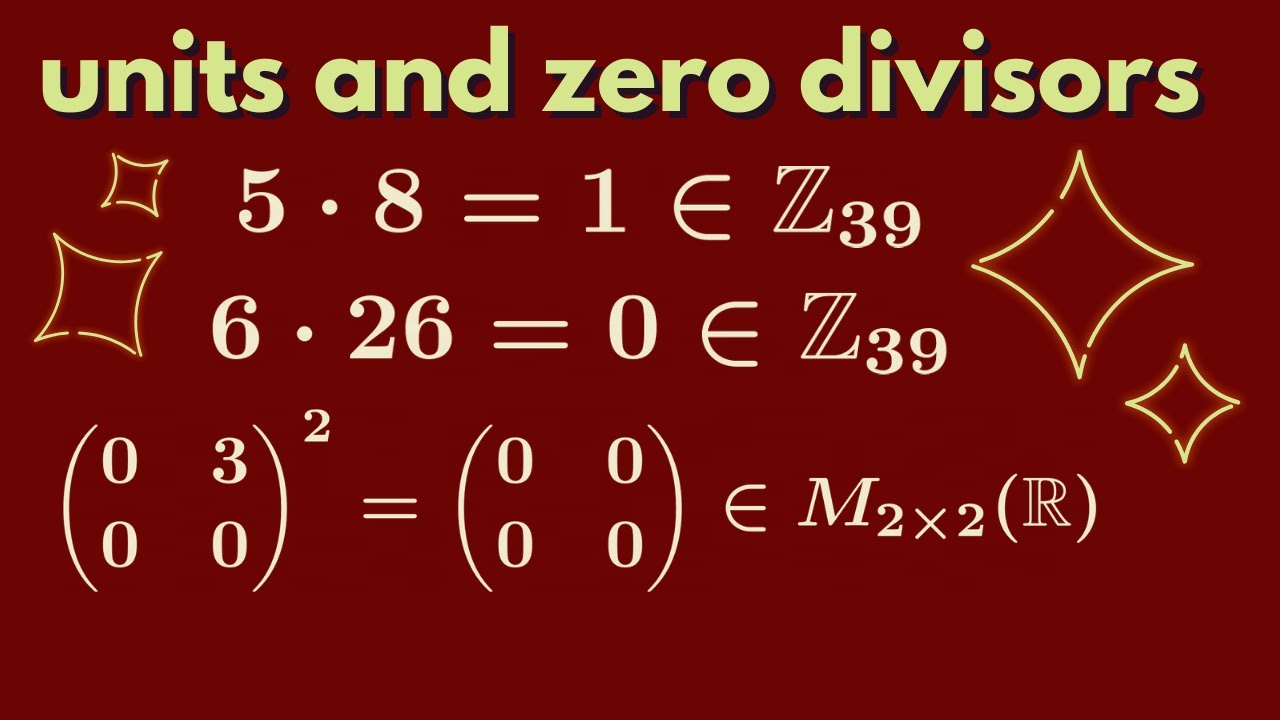Definition of a Zero Divisor and Properties and Examples of Zero Divisors

Definition of a Zero Divisor

In mathematics, a zero divisor refers to an element in a ring that multiplied by another non-zero element equals zero. More precisely, let’s consider a ring R and let a, b ∈ R be elements such that a ≠ 0 and b ≠ 0. If a * b = 0, then a or b (or both) is referred to as a zero divisor.

In simpler terms, a zero divisor is an element in a ring that can be multiplied by a non-zero element to produce zero. This implies that there exist non-zero elements whose product is zero, violating one of the fundamental properties of a ring where the product of any two non-zero elements should always be non-zero.

Properties and Examples of Zero Divisors

A zero divisor is an element in a mathematical structure, such as a ring or a module, that can multiply with another non-zero element to give a result of zero.

In the context of rings, zero divisors are elements that, when multiplied with another non-zero element, yield the additive identity element of the ring, which is usually denoted by 0. In other words, if a and b are elements of a ring and a * b = 0, where 0 represents the additive identity, then a and b are zero divisors.

Here are some examples of zero divisors:

1. In the ring of integers modulo 6 (ℤ₆), the elements 2 and 3 are zero divisors because 2 * 3 ≡ 0 mod 6.

2. In the ring of real numbers, the elements 0 and 4 are zero divisors because 0 * 4 = 0.

3. In the ring of 2×2 matrices with real entries, the matrix [[1, 0], [0, 0]] is a zero divisor because it can be multiplied with the non-zero matrix [[0, 1], [0, 0]] to give the zero matrix.

4. In the polynomial ring ℤ₃[x], where the coefficients are integers modulo 3, the polynomial 2x + 1 is a zero divisor because it can be multiplied with the non-zero polynomial 2x + 2 to yield 0.

In general, zero divisors can arise in any ring that does not have the property of being an integral domain. An integral domain is a nonzero commutative ring in which the product of any two nonzero elements is also nonzero.

Zero Divisors in Different Number Systems

Zero divisors are elements in a number system that, when multiplied by another element, result in zero. In other words, they are non-zero elements that have a product of zero with at least one other non-zero element.

In the decimal number system (base 10), there are no zero divisors. This means that if you multiply any non-zero number by another non-zero number, the product will never be zero. For example, in base 10, 5 * 2 = 10, which is not equal to zero.

However, in other number systems, such as modular arithmetic or finite fields, zero divisors can exist. For example, in the modulo 6 arithmetic system (also called Z/6Z), the set of numbers 2 and 3 are zero divisors. If we multiply 2 * 3 (mod 6), the result is 0. Similarly, in the finite field of integers modulo 9 (denoted as Z/9Z), the numbers 3 and 6 are zero divisors since 3 * 6 (mod 9) equals 0.

It is important to note that zero divisors violate the fundamental property of a field, which states that every non-zero element must have a unique multiplicative inverse. In other words, if a number has a zero divisor, it cannot have a unique reciprocal.

The Relationship Between Zero Divisors and Unit Elements

In mathematics, zero divisors and unit elements have an interesting relationship.

First, let’s define what zero divisors and unit elements are. Zero divisors are nonzero elements in a set that, when multiplied by another nonzero element, yield a product of zero. In other words, if a and b are nonzero elements in a set, and a * b = 0, then a and b are zero divisors.

On the other hand, a unit element, also known as an identity element or a multiplicative inverse, is an element in a set that, when multiplied by another element, yields the same element as the result. In other words, if a is an element in a set, and a * b = b * a = b for all elements b in the set, then a is a unit element.

The relationship between zero divisors and unit elements is that a nonzero element in a set cannot be both a zero divisor and a unit element at the same time. This is because if an element a is a zero divisor, there exists a nonzero element b such that a * b = 0. However, if a is a unit element, then a * b = b, not 0.

Therefore, in any set with zero divisors, there are no unit elements. Similarly, in any set with unit elements, there are no zero divisors. This relationship can be observed in various algebraic structures such as rings, fields, and groups.

It is worth noting that not all sets may have both zero divisors and unit elements. Some sets may have zero divisors but no unit elements, while others may have unit elements but no zero divisors. It depends on the specific properties of the set and the operations defined on it.

Applications and Importance of Zero Divisors in Mathematics

In mathematics, zero divisors are elements of a algebraic structure, such as a ring, that when combined with another element, produce the additive identity (usually denoted as 0). More formally, an element a is said to be a zero divisor if there exists a non-zero element b such that ab = 0.

Zero divisors are of importance in various areas of mathematics, including algebra, number theory, and abstract algebra. Here are a few applications and reasons why zero divisors are significant:

1. Geometry and Graph Theory: Zero divisors can be used to study properties of graphs and networks. In graph theory, a zero divisor can represent a nontrivial partition of a graph. For example, in a coloring problem, zero divisors can help determine the minimum number of colors required to color the vertices of a graph.

2. Factorization in Rings: In algebraic structures, such as rings, zero divisors play a crucial role in factorization. If zero divisors exist, it implies that the ring does not have the property of unique factorization. This property is essential in number theory for prime factorization and determining divisibility rules.

3. Study of Nilpotency: Zero divisors provide a connection to the study of nilpotency, which is a property of elements that, when raised to a certain power, result in zero. Nilpotent elements are closely related to zero divisors, and their properties can be significant in algebraic structures and representation theory.

4. Algebraic Structure: Zero divisors are crucial in defining rings and other algebraic structures. They generate non-trivial substructures that influence the behavior and properties of the overall structure. Understanding and characterizing zero divisors aid in the classification and analysis of these structures.

5. Applications in Coding Theory and Cryptography: Zero divisors are used in coding theory, which deals with error detection and correction in communication systems. Zero divisors help design error-correcting codes and provide a mathematical foundation for encryption algorithms in cryptography.

In summary, zero divisors have applications in various fields of mathematics, ranging from algebraic structures to graph theory and coding theory. They play an important role in factorization, nilpotency, and determining the properties and behaviors of algebraic structures.

Topics related to Zero divisor