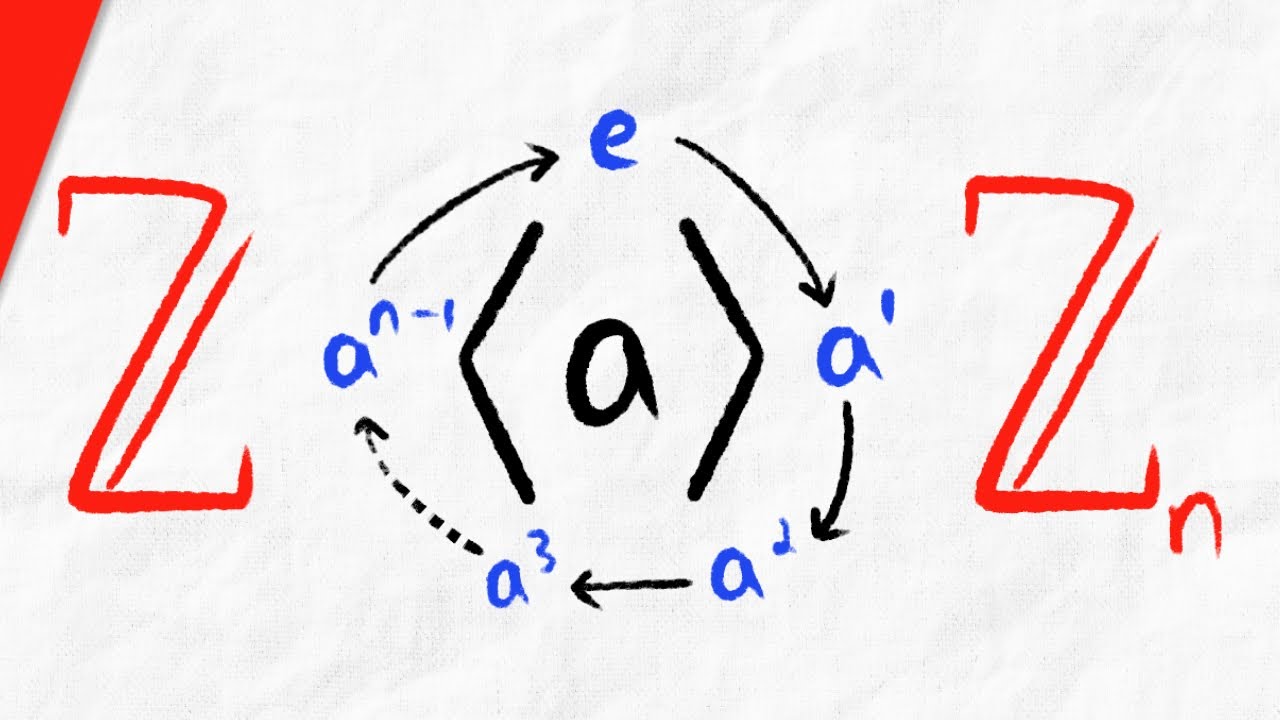
Definition of Cyclic Group and Properties of Cyclic Groups

Definition of Cyclic Group

A cyclic group is a mathematical concept in abstract algebra. It is a group that is generated by a single element, called a generator, and all other elements in the group can be obtained by repeatedly applying the group operation to the generator. In other words, every element of a cyclic group can be expressed as a power of the generator.

Formally, a cyclic group is denoted as ⟨g⟩ or , where g is the generator. The group operation is typically denoted as multiplication, and the group is written multiplicatively. The operation can be represented as g^n, where n is an integer. The generator g can be an element of any mathematical set, such as integers, rational numbers, or complex numbers.

Cyclic groups have several important properties. They are always abelian, meaning that the group operation is commutative. Additionally, the order of a cyclic group, which is the number of elements in the group, is equal to the order of the generator.

Cyclic groups are widely studied in various branches of mathematics, including number theory, algebraic geometry, and cryptography. They have important applications in solving mathematical problems and understanding the structure of other mathematical objects.

Properties of Cyclic Groups

A cyclic group is a group that is generated by a single element. This means that all other elements in the group can be obtained by repeatedly applying the group operation to the generator element.

Some properties of cyclic groups include:

1. Unique generator: Every cyclic group has a unique generator. This means that if a group is cyclic, there exists a single element that can generate the entire group.

2. Finite or infinite: Cyclic groups can be either finite or infinite. A finite cyclic group has a finite number of elements, while an infinite cyclic group has an infinite number of elements.

3. Order: The order of a cyclic group is the number of elements in the group. For a cyclic group generated by an element “a”, the order of the group is equal to the smallest positive integer “n” such that a^n = e, where e is the identity element of the group.

4. Subgroups: Cyclic groups have a unique subgroup for every divisor of the group’s order. This means that if the order of a cyclic group is “n”, it has exactly “n” subgroups.

5. Group isomorphism: Every cyclic group of order “n” is isomorphic to the additive group of integers modulo “n” (denoted as Z/nZ). This means that the structure and properties of a cyclic group can be equivalently represented using integers and addition modulo “n”.

6. Closure property: Cyclic groups are closed under the group operation. This means that if “a” and “b” are elements of a cyclic group, then their product “ab” is also an element of the group.

7. Identity element: Every cyclic group has an identity element, denoted as “e”. This element acts as the neutral element under multiplication or addition, depending on the group operation.

8. Inverse element: Every element in a cyclic group has an inverse element. This means that for every element “a” in the group, there exists another element “b” such that ab = ba = e, where e is the identity element.

Examples of Cyclic Groups

1) The integers under addition (denoted as Z) form a cyclic group, where the generator is 1. This means that every integer can be represented as a power of 1, such as 1, 2, 3, …, or -1, -2, -3, ….

2) The group of residues modulo n (denoted as Z/nZ) is a cyclic group with n elements, where n is a positive integer. For example, the group Z/5Z with elements {0, 1, 2, 3, 4} is cyclic, and any element can be a generator.

3) The group of invertible elements modulo n (denoted as U(n)) is a cyclic group if and only if n is equal to 1, 2, 4, a power of an odd prime, or twice a power of an odd prime. For example, U(7) with elements {1, 2, 3, 4, 5, 6} is cyclic, and any element can be a generator.

4) The group of rotations of a regular polygon (denoted as D(n)) is a cyclic group, where n is the number of sides of the polygon. For example, D(3) for an equilateral triangle has elements {0°, 120°, 240°} and is cyclic, with any element being a generator.

Order of Elements in Cyclic Groups

In a cyclic group, the order of elements refers to the number of times an element needs to be repeated to return to the group’s identity element, usually denoted as “e.”

To determine the order of an element in a cyclic group, it is necessary to repeatedly multiply or combine the element with itself until the identity element is obtained.

For example, let’s consider a cyclic group generated by an element “g.”

If g^2 = g * g = e (identity element), then the order of g is 2.

If g^3 = g * g * g = e, then the order of g is 3.

In general, the order of an element “g” in a cyclic group is denoted as |g|.

The order of an element always divides the order of the cyclic group. This means that if a cyclic group has “n” elements, the order of any element in the group can be an integer divisor of “n.”

Applications of Cyclic Groups

Cyclic groups have various applications in mathematics and other fields. Here are a few examples:

1. Cryptography: Cyclic groups play a crucial role in the field of cryptography, which involves securing and protecting information. They are often used in protocols such as the Diffie-Hellman key exchange and the ElGamal encryption system, where the algebraic properties of cyclic groups provide a secure method for key generation and encryption.

2. Coding theory: Cyclic codes, which are linear error-correcting codes generated by cyclic groups, are widely used in error detection and correction algorithms. These codes have the advantage of efficient encoding and decoding procedures, making them suitable for applications in data transmission and storage.

3. Number theory: The study of cyclic groups is closely tied to number theory, particularly in the field of modular arithmetic. The properties of cyclic groups help in understanding prime numbers, Euler’s totient function, and the structure of residue classes modulo n.

4. Algebraic geometry: In the study of algebraic curves and surfaces, cyclic groups offer insights into their structure and properties. For example, the group of rational points on an elliptic curve often forms a cyclic group, which has implications for cryptography and coding theory, as mentioned earlier.

5. Physics: Cyclic groups find application in various areas of physics, including quantum mechanics and symmetry groups. For instance, cyclic groups are used to describe rotational symmetry in quantum systems and to analyze the behavior of particles in specific physical systems.

6. Computer science: Cyclic groups have applications in discrete mathematics and computer science, particularly in the analysis of algorithms and data structures. They are used in problems related to graph theory, network routing, and distributed computing.

7. Group theory: Cyclic groups serve as fundamental examples in the study of abstract algebra and group theory. They provide a simple and accessible context for exploring the concepts of group structure, subgroups, and group actions, which are foundational in many branches of mathematics.

Topics related to Cyclic group