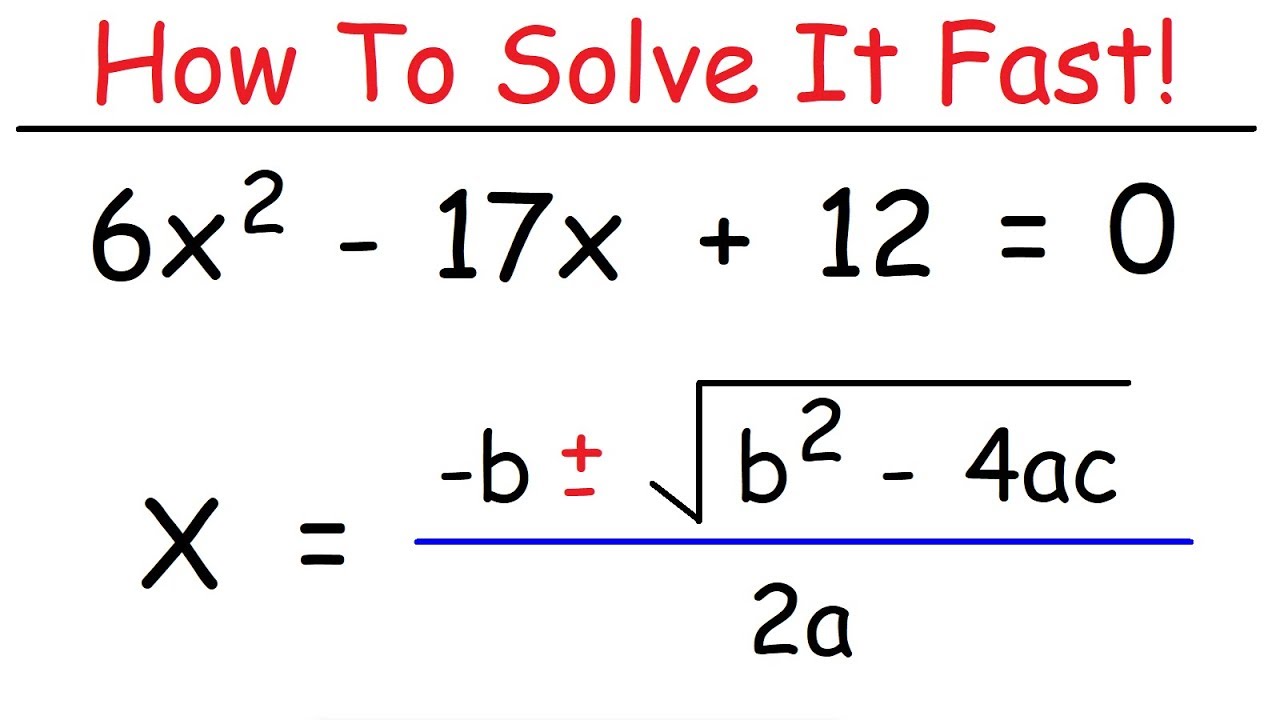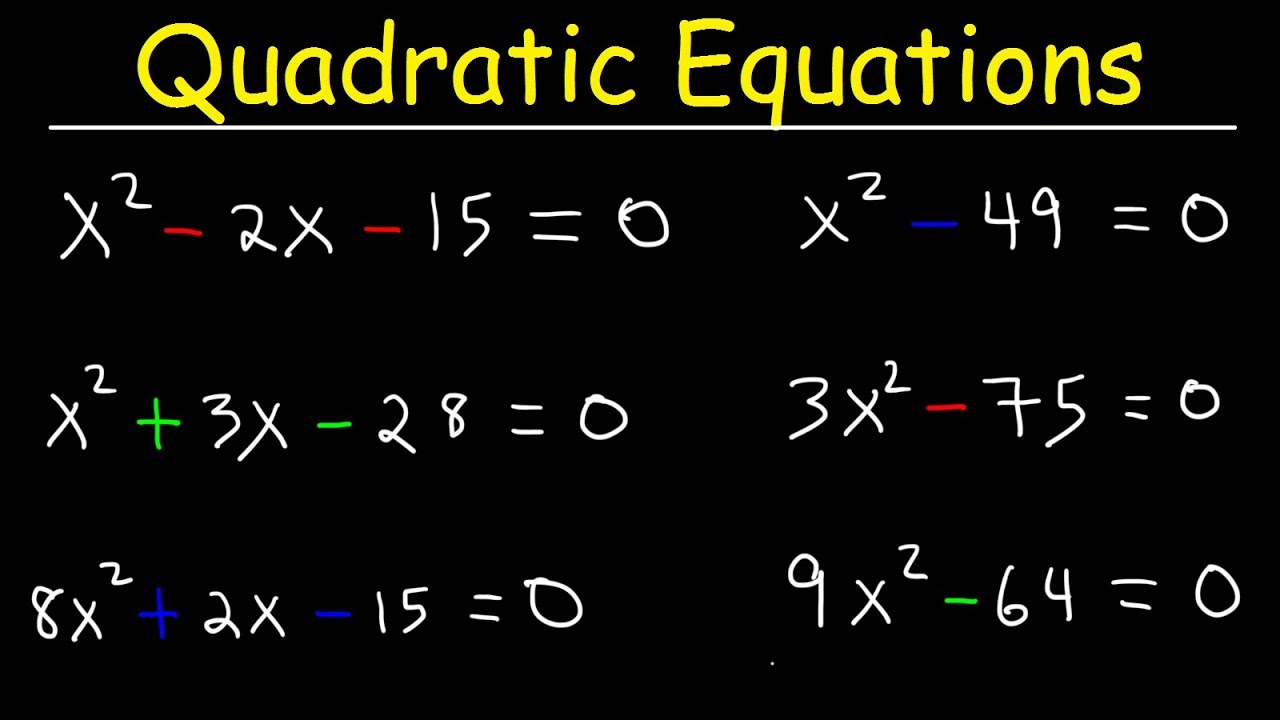Definition of Quadratic and Solving Quadratic Equations

Definition of Quadratic

The word “quadratic” can have two meanings:

1. As an adjective, “quadratic” refers to something that is related to the mathematical concept of a quadratic equation or quadratic function. In mathematics, a quadratic equation is a polynomial equation of the second degree, meaning that it contains the variable raised to the power of 2. It can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. A quadratic function, on the other hand, is a mathematical function that can be expressed as f(x) = ax^2 + bx + c, where f(x) represents the output value for a given input value x.

2. As a noun, “quadratic” refers to a quadratic polynomial or expression. It is a polynomial of the second degree, meaning that it contains a term with the variable raised to the power of 2. For example, the expression 3x^2 + 2x + 1 is a quadratic because it has a term (3x^2) with the variable x raised to the power of 2.

In both cases, the term “quadratic” is associated with mathematical equations and functions that involve a squared term.

Solving Quadratic Equations

To solve quadratic equations, you can use either factoring, the quadratic formula, or completing the square methods.

1. Factoring:

First, rewrite the equation in the form ax^2 + bx + c = 0, where a, b, and c are coefficients.

Then, try to factor the quadratic equation into two binomial expressions.

Once factored, set each binomial expression equal to zero and solve for x.

2. Quadratic Formula:

The quadratic formula is given by x = (-b ± √(b^2 – 4ac)) / 2a.

Identify the values of a, b, and c in the quadratic equation ax^2 + bx + c = 0.

Substitute the values of a, b, and c into the quadratic formula and simplify.

Calculate the two possible values of x using the plus or minus sign.

3. Completing the Square:

Rearrange the quadratic equation to the form ax^2 + bx + c = 0.

Move the constant term (c) to the right side of the equation.

Divide the equation by the coefficient of x^2 (a) to make its coefficient 1.

Take half of the coefficient of x (b/2) and square it.

Add the squared term to both sides of the equation.

Rewrite the trinomial as a perfect square and solve for x.

Take the square root of both sides to find the values of x.

Once you have solved the quadratic equation, you will obtain the values of x, which represent the solutions or roots of the quadratic equation.

Graphing Quadratic Functions

Quadratic functions are a type of polynomial function that can be represented by a quadratic equation of the form f(x) = ax^2 + bx + c, where a, b, and c are constants. When graphed, quadratic functions form a curve called a parabola.

To graph a quadratic function, you can follow these steps:

1. Determine the vertex of the parabola. The vertex of a quadratic function with equation f(x) = ax^2 + bx + c can be found using the formula x = -b/2a. The x-coordinate of the vertex is the value that minimizes or maximizes the quadratic function, depending on the sign of the coefficient a. The y-coordinate of the vertex can be found by substituting the x-coordinate into the equation.

2. Find the axis of symmetry. The axis of symmetry is a vertical line that passes through the vertex of the parabola. The equation of the axis of symmetry is x = -b/2a.

3. Find the y-intercept. The y-intercept is the point at which the parabola intersects the y-axis. To find the y-intercept, substitute x = 0 into the equation and solve for y.

4. Determine the x-intercepts (also known as roots or zeros). The x-intercepts are the points at which the parabola intersects the x-axis. To find the x-intercepts, set f(x) = 0 and solve the quadratic equation for x.

5. Plot the vertex, axis of symmetry, y-intercept, and x-intercepts on a coordinate plane. Connect the points with a smooth curve to form the parabola.

6. Determine additional points. You may choose to find a few more points around the vertex to better understand the shape of the parabola. To do this, you can substitute different x-values into the equation to find the corresponding y-values.

Remember that the behavior of the parabola depends on the sign of the coefficient a. If a > 0, the parabola opens upward and has a minimum value at the vertex. If a

By following these steps, you can graph quadratic functions and visualize their shape and characteristics.

Applications of Quadratic Equations

Quadratic equations have various applications in different fields. Here are a few examples:

1. Physics: Quadratic equations can be used to model physical phenomena such as projectile motion, motion under gravity, and the behavior of springs. The equation can help calculate quantities like time of flight, maximum height, range, and position of an object at any given time.

2. Engineering: Quadratic equations are used to solve problems related to engineering, such as finding the optimal shape for a structure, analyzing the behavior of mechanical systems, and calculating the equilibrium points in electrical circuits.

3. Economics: Quadratic equations play a role in economics by helping to determine the optimal levels of production and employment. They can also be used to analyze supply and demand curves, profit and cost functions, and determine maximum or minimum values in economic models.

4. Finance: Quadratic equations are used in finance to calculate elements like the yield on certain investments, the value of options and derivatives, and determining optimal portfolio allocations.

5. Computer graphics: Quadratic equations are used extensively in computer graphics to model and render smooth curves and surfaces. They can be used to draw parabolas, ellipses, and other shapes.

6. Probability: Quadratic equations are utilized in probability theory to solve problems involving probability distributions and statistical analysis. They can help determine the expected value, variance, and other statistical properties of random variables.

7. Medicine: Quadratic equations are utilized in model fitting for pharmaceutical research, drug dosage calculations, and determining the kinetics of drug absorption and elimination from the body.

These are just a few examples of how quadratic equations are applied in various fields. The versatility and utility of quadratic equations make them an essential tool in solving a wide range of problems across different disciplines.

Advanced Topics in Quadratics

Advanced Topics in Quadratics

1. Complex Solutions: Quadratic equations can have complex solutions, involving imaginary numbers. These solutions occur when the discriminant, b^2 – 4ac, is negative. Understanding complex solutions is important in various fields, such as electrical engineering and quantum mechanics.

2. Quadratic Inequalities: Quadratic inequalities involve quadratic expressions with inequality symbols (, ≤, ≥) instead of equality symbols. Solving quadratic inequalities requires finding the intervals for which the expression is greater or lesser than zero. This topic is significant in optimization problems and real-world applications.

3. Higher Degree Quadratics: While quadratic equations have second-degree terms (x^2), higher degree quadratics include terms with higher exponents. These equations can have multiple solutions and complex patterns. Analyzing higher degree quadratics involves studying polynomial functions and their properties.

4. Conic Sections: Quadratic equations also play a vital role in the study of conic sections, which are geometric shapes formed by intersecting a plane with a cone. The two-dimensional conic sections include parabolas, ellipses, and hyperbolas. Understanding the quadratic equations that govern these curves is crucial in mathematics and physics.

5. Vertex Form and Transformations: Quadratic equations can be written in vertex form, which provides information about the vertex (minimum/maximum point) of the parabola. By using vertex form, it is possible to observe transformations such as translations, reflections, and stretches/shrinks of the parabola. This topic is relevant in graphing and analyzing quadratic functions.

6. Solving for Parameters and Applications: Quadratic equations often involve parameters (variables other than x), which can represent various real-world quantities. Solving for these parameters allows us to determine relationships and make predictions across different scenarios. This aspect of quadratics is important in fields such as physics, economics, and engineering.

7. Quadratic Patterns and Sequences: Quadratic equations can generate sequences and patterns that exhibit quadratic behavior. Recognizing these patterns and finding the nth term formula (general formula for an nth term in a sequence) involve working with quadratic equations. Understanding quadratic patterns is essential in number theory and algebraic reasoning.

8. Optimization and Quadratic Models: Quadratic models involve using quadratic equations to optimize a particular objective function. This could include maximizing profit, minimizing cost, or finding the maximum height of a projectile. Optimization problems with quadratic models are commonly encountered in business, engineering, and physics.

Topics related to Quadratic