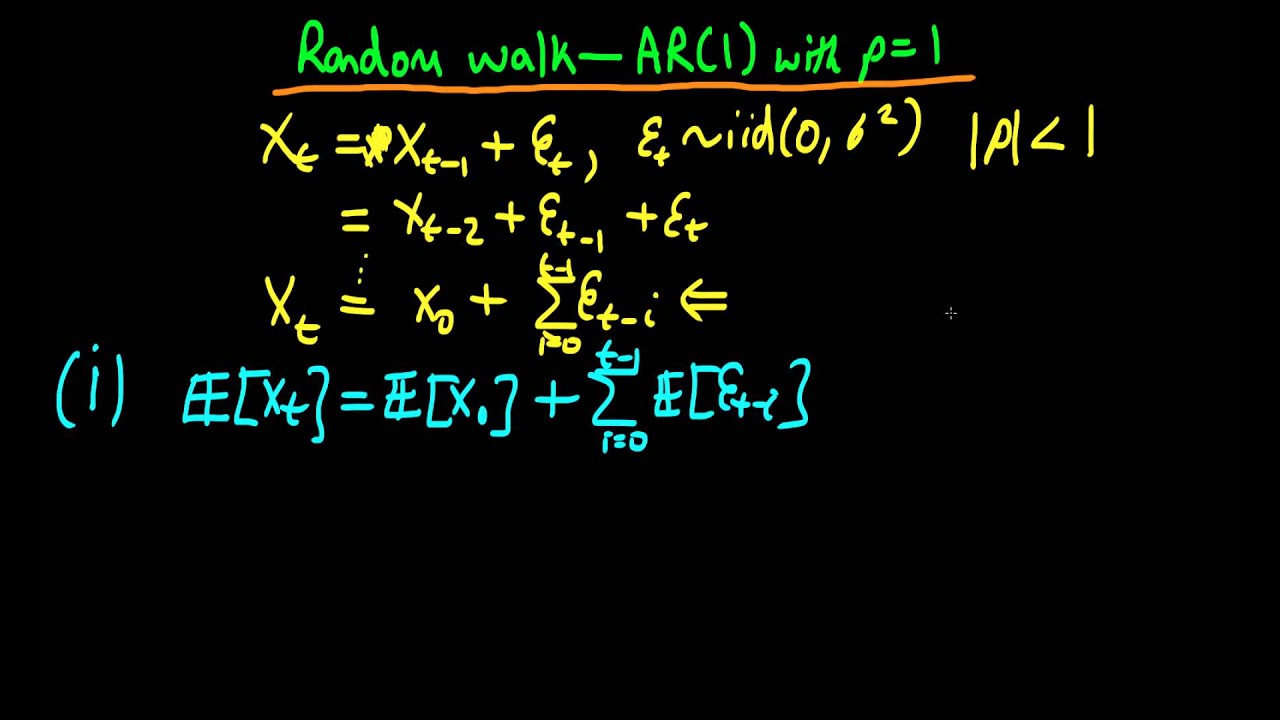Definition of Random Walk and Mathematics behind Random Walk

Definition of Random Walk

Random Walk is a mathematical concept that describes the movement of a variable or data set in a random or unpredictable fashion. It refers to a sequence of random steps or changes in value, where each step is independent of the previous step and has an equal probability of going in any direction.

In the context of finance and economics, a Random Walk often describes the movement of the price of a financial instrument, such as a stock or currency, where the future price changes are unpredictable and follow a random pattern. This means that the future price cannot be reliably predicted based on past price movements or any other information.

The concept of Random Walk has various applications, such as in modeling the behavior of stock prices in the efficient market hypothesis, simulating random processes in physics and biology, and analyzing random sampling techniques in statistics.

Mathematics behind Random Walk

The mathematics behind a random walk is based on the concept of a stochastic process, where the position of an object is determined by a series of random steps.

In a simple random walk, the object, often represented as a point, starts at a given position and then takes a series of steps in random directions. Each step is typically assumed to have equal probabilities of moving in different directions, such as up, down, left, or right. These steps are usually independent of each other, meaning that the outcome of one step does not affect the outcome of the next.

Mathematically, a simple random walk can be modeled as a sequence of random variables, where each variable determines the direction of the next step. These random variables are often described using probability distributions, such as a discrete uniform distribution for equal probabilities of each direction.

The position of the object after a certain number of steps can be described by adding up the individual steps taken. For example, if the object takes steps of length 1, then the position after n steps is the sum of n random variables.

The behavior of a random walk can be analyzed using various mathematical techniques. One important concept is the expected value, which represents the average position of the object after a certain number of steps. In a symmetric random walk, where the probabilities of moving in different directions are equal, the expected value remains the same over time.

Another important concept is the variance, which measures the spread or dispersion of the random walk. The variance can be used to determine the likelihood of the object reaching certain positions after a given number of steps.

Random walks have numerous applications in various fields of science and mathematics, such as finance, physics, computer science, and biology. They provide a simple yet powerful model for studying systems that undergo random movements or fluctuations.

Applications of Random Walk

Random walk is a concept commonly used in mathematics and physics, but it also finds various applications in real-world scenarios. Here are some of the key applications of random walk:

1. Financial Markets: Random walk models are frequently employed in finance to study the unpredictable movements of stock prices. The hypothesis of the efficient market suggests that stock prices follow a random walk, implying that past price movements do not predict future price changes. This concept aids in the development of investment strategies and risk management techniques.

2. Biology and Genetics: Random walks are used to model the behavior of molecules and particles in biological systems. For example, the movement of bacteria, viruses, or pollutants in water can be simulated using random walk models. In genetics, random walks are employed to model the path of gene sequences, mutation occurrences, and DNA sequencing.

3. Optimization Algorithms: Random walk algorithms are utilized in optimization problems to find the optimal solution among a large set of possibilities. These algorithms involve iteratively exploring potential solutions by randomly navigating through the solution space to Monte Carlo samples. Random walk-based optimization algorithms are widely used in fields like operations research, computer science, and engineering.

4. Image Analysis: Random walks are employed in image segmentation, a process of dividing an image into different regions to isolate and extract objects of interest. By considering image pixels as nodes and their similarities as edge weights, random walk algorithms can determine regions within an image that exhibit similar features.

5. Social Network Analysis: Random walks have applications in studying social networks, such as determining influence or popularity measures in online communities. Random walk-based algorithms can identify influential nodes or recommend relevant connections based on the random exploration of the network structure.

6. Physics and Chemistry: Random walks are utilized in simulating the movement of particles in various physical and chemical processes. For example, molecular dynamics simulations often employ random walk-based algorithms to model the movements and interactions of atoms and molecules in a system.

Overall, random walks find applications in diverse fields, including finance, biology, optimization, image analysis, social networks, physics, and chemistry. Due to their stochastic nature, random walk models provide valuable insights into complex systems and aid in solving real-world problems.

Limitations and extensions of Random Walk

The random walk is a mathematical model that determines the path taken by an object that undergoes a series of random steps. It has various limitations and extensions that should be considered when using it in different contexts.

Limitations:

1. Lack of memory: In a standard random walk, each step is independent of previous steps. This means that the model does not consider any past history or context when determining future steps. This limitation makes it less suitable for situations where memory or persistence of direction is important.

2. Gaussian assumption: Random walks often assume that the step size or direction follows a Gaussian (normal) distribution. While this assumption may be reasonable in some cases, it may not accurately reflect the actual distribution in certain real-world scenarios. In such cases, alternative distributions or modified random walk models may be more appropriate.

3. No constraints: Random walks do not incorporate any constraints or limitations on the movement. In reality, there may be barriers, boundaries, or other conditions that restrict the movement of the object being modeled. These constraints are not accounted for in a standard random walk and must be considered separately.

Extensions:

1. Drift: To overcome the lack of memory in standard random walks, a drift term can be introduced. A drift represents a systematic bias or trend in the movement, which can be added to each step to provide persistence. This extension allows for the incorporation of previous steps’ information into future steps.

2. Correlated steps: In some cases, steps in a random walk may be correlated, meaning that each step depends on the previous step or a combination of past steps. This extension helps capture the influence of historical data and can be useful in situations with memory or persistence.

3. Spatial and temporal variations: Random walk models can be extended to incorporate spatial or temporal variations in step size or direction. This allows for more realistic modeling in scenarios where the environment or external factors affect the randomness of the movement.

4. Constrained random walks: By introducing constraints or boundaries, random walks can be modified to reflect real-world limitations. For example, in ecology, random walks are often combined with landscape features or barriers to model animal movement within a specific habitat.

5. Fractional random walks: Fractional random walks generalize the concept of random walks by allowing for non-integer step lengths or power-law distributions of step sizes. This extension is particularly useful in situations where the movement exhibits long-range dependence or scaling properties.

Overall, while the random walk serves as a fundamental model for random processes, its limitations and extensions demonstrate its versatility and the need for modifications in different contexts to capture the complexity of real-world phenomena.

Conclusion

In conclusion, a random walk refers to a mathematical model that describes the unpredictable movement of a variable over time. It is characterized by a series of steps taken in a random manner, where each step is independent of the previous one. Random walks have found applications in a variety of fields, including finance, physics, biology, and computer science.

One key finding in random walk theory is that the expected value of a random walk is often zero, indicating that there is no overall trend in the variable being studied. This result has important implications for financial markets, as it suggests that stock prices, for example, cannot be predicted with certainty based on past prices alone.

Another important concept related to random walks is the concept of diffusion. Random walks can be seen as a type of diffusion process, where the variable being studied spreads out in a random manner over time. This diffusion behavior is observed in various natural phenomena, such as the movement of particles in a fluid or the spread of diseases in a population.

Overall, random walks provide a useful framework for understanding the inherent randomness and unpredictability present in many real-world systems. By studying the properties of random walks, researchers and practitioners can gain insights into various phenomena and make more informed decisions in the face of uncertainty.

Topics related to Random Walk