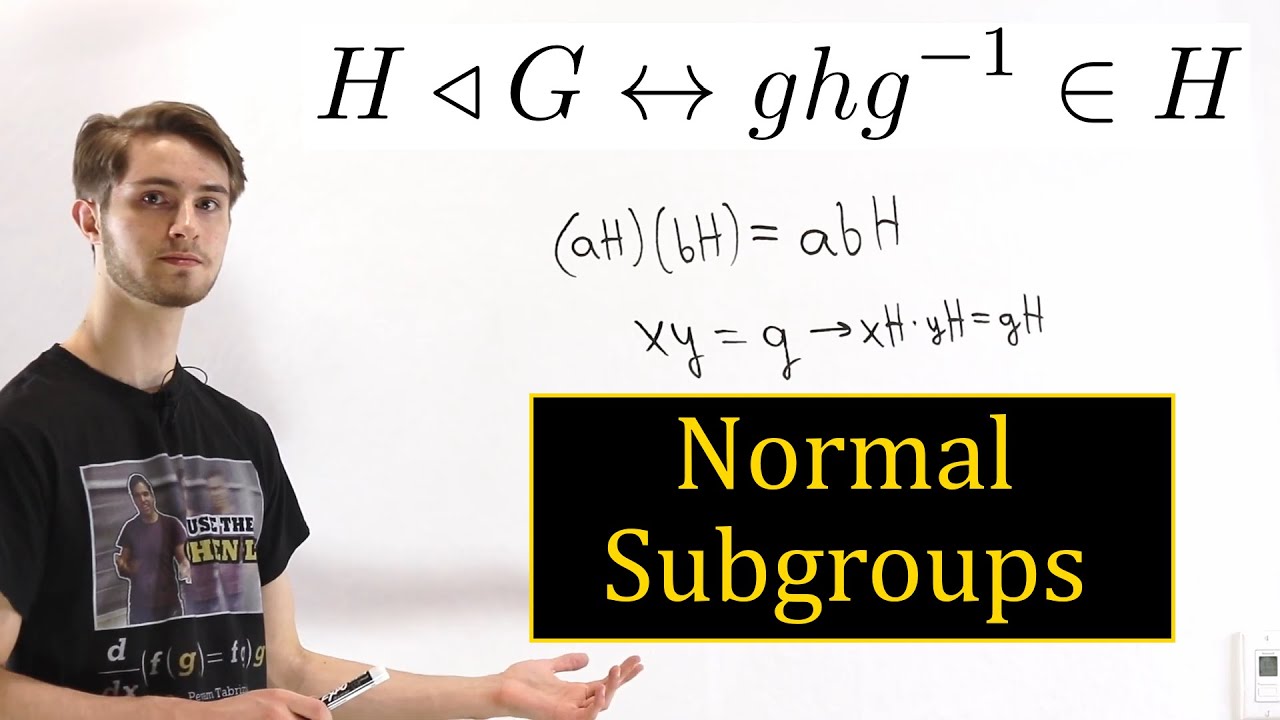Introduction and Definition of a Normal Subgroup

Introduction

Introduction:

A normal subgroup is a special type of subgroup in abstract algebra, specifically in the context of group theory. Normal subgroups play a crucial role in understanding the structure and properties of groups.

Definition of Normal Subgroup:

Let G be a group and H be a subgroup of G. The subgroup H is said to be normal, denoted as H ∆ G, if for every element a in G and every element h in H, the conjugate of h by a is also in H, that is, aha^(-1) ∈ H.

Alternatively, a subgroup H is normal if and only if it is invariant under conjugation by elements of G.

Properties of Normal Subgroups:

1. Normal subgroups are a means of partitioning a group G into distinct cosets. The index of a normal subgroup H in G, denoted as [G:H], represents the number of distinct cosets of H in G.

2. Normal subgroups are closed under the operation of taking inverses. If H is a normal subgroup of a group G, then for any element h in H, its inverse h^(-1) is also in H.

3. The intersection of any collection of normal subgroups of G is itself a normal subgroup of G.

4. If H is a normal subgroup of G, then the quotient group G/H inherits a natural group structure. The elements of G/H are the right cosets of H in G, and the group operation is defined as the coset multiplication.

5. Normal subgroups have a fundamental connection with homomorphisms. The kernel of a group homomorphism is always a normal subgroup.

Applications of Normal Subgroups:

1. Normal subgroups are essential in the study of factor groups, which provide a way to simplify and understand group structures.

2. Normal subgroups are used to define and understand important group properties, such as simple groups and solvable groups.

3. Normal subgroups have applications in various areas of mathematics, including number theory, algebraic geometry, and cryptography.

In conclusion, normal subgroups are a fundamental concept in group theory that allows for a deeper understanding of the structure and properties of groups. Their properties and applications make them an important topic in abstract algebra.

Definition of a Normal Subgroup

A normal subgroup, denoted as N, is a subgroup of a group G such that for any element g in G, the conjugates of N by g are also contained in N. In other words, if N is a normal subgroup of G, then for every g in G, the set gNg^(-1) is also a subgroup of G, and it is equal to N.

This can also be expressed as follows: for any element g in G and n in N, the element gng^(-1) is also in N.

A normal subgroup is an important concept in group theory as it allows for the definition of quotient groups, which are formed by partitioning the elements of a group by their equivalence under a normal subgroup.

Properties of Normal Subgroups

A normal subgroup is a subgroup of a group that is invariant under conjugation by any element in the group. In other words, for any element g in the group and any element h in the normal subgroup, the conjugate ghg^(-1) is also in the normal subgroup.

Properties of normal subgroups include:

1. Closure under conjugation: If N is a normal subgroup of G, then for any element g in G and any element n in N, the conjugate gng^(-1) is also in N.

2. Preservation of normality under homomorphisms: If N is a normal subgroup of G and f is a homomorphism from G to another group H, then the image of N under f, denoted as f(N), is also a normal subgroup of H.

3. Quotient group: If N is a normal subgroup of G, then the set of left cosets of N in G forms a group, called the quotient group G/N. The operation in the quotient group is defined as (gN)(hN) = (gh)N, where g, h belong to G.

4. Factorization property: If N is a normal subgroup of G, then every element of the quotient group G/N can be written as a product of the form gN, where g is an element in G.

5. Intersection of normal subgroups: If N and M are both normal subgroups of G, then the intersection N ∩ M is also a normal subgroup of G.

6. Normality is transitive: If H is a normal subgroup of N, and N is a normal subgroup of G, then H is a normal subgroup of G.

These properties are important in the study of group theory, as they help provide a deeper understanding of the structure and behavior of groups and their subgroups.

Examples of Normal Subgroups

1. In the group of integers under addition, the subgroup of even integers is a normal subgroup. This is because if we take any integer, add an even integer to it, and then subtract the same even integer, we will still end up with an even integer.

2. In the group of real numbers under addition, the subgroup of rational numbers is a normal subgroup. This is because if we take any real number, add a rational number to it, and then subtract the same rational number, we will still end up with a rational number.

3. In the group of symmetric permutations of a set, the subgroup of all identity permutations is a normal subgroup. This is because the identity permutation commutes with any other permutation, meaning that if we conjugate the identity permutation by any other permutation, the result is still the identity permutation.

4. In the group of 2×2 invertible matrices under matrix multiplication, the subgroup of all diagonal matrices is a normal subgroup. This is because if we take any invertible matrix, multiply it by a diagonal matrix, and then multiply by the inverse of the diagonal matrix, we will still end up with a diagonal matrix.

Applications of Normal Subgroups

Normal subgroups have various applications in group theory and other areas of mathematics. Here are some of the key applications:

1. Quotient groups: One of the main applications of normal subgroups is in constructing quotient groups. If N is a normal subgroup of a group G, then the set of cosets of N in G forms a group under the operation defined by (Ng)(Nh) = N(gh), where g and h are elements of G. This new group, denoted G/N, is called the quotient group of G by N. Quotient groups have many important properties and are widely studied in group theory.

2. Isomorphism theorems: The isomorphism theorems in group theory provide important results related to normal subgroups. These theorems establish correspondences between subgroups, normal subgroups, and quotient groups. They allow us to relate the structures of different groups through homomorphisms and isomorphisms.

3. Factor groups: A factor group, also known as a modular group or group extension, is a group that is obtained from another group by adding new elements subject to certain relations. Normal subgroups play a crucial role in the construction of factor groups. Given a group G and a normal subgroup N, the factor group G/N consists of the cosets of N in G with a specific group operation defined on them. Factor groups have applications in various areas, including algebraic number theory and Galois theory.

4. Character theory: Normal subgroups are fundamental in the study of character theory, a branch of representation theory. Character theory deals with the representation of a group by a set of characters, which are functions on the group that satisfy certain properties. Normal subgroups allow us to decompose the characters of a group into irreducible characters, providing valuable information about the group’s structure.

5. Homomorphisms: Normal subgroups have a close connection with group homomorphisms. In particular, if N is a normal subgroup of a group G, then there exists a homomorphism from G onto the quotient group G/N. This homomorphism is called the canonical projection or quotient map. Normal subgroups help to define and analyze the behavior of homomorphisms between groups.

These are just a few applications of normal subgroups in mathematics. They have a wide range of uses in understanding group structure, solving equations, and exploring symmetries in various mathematical contexts.

Topics related to Normal subgroup