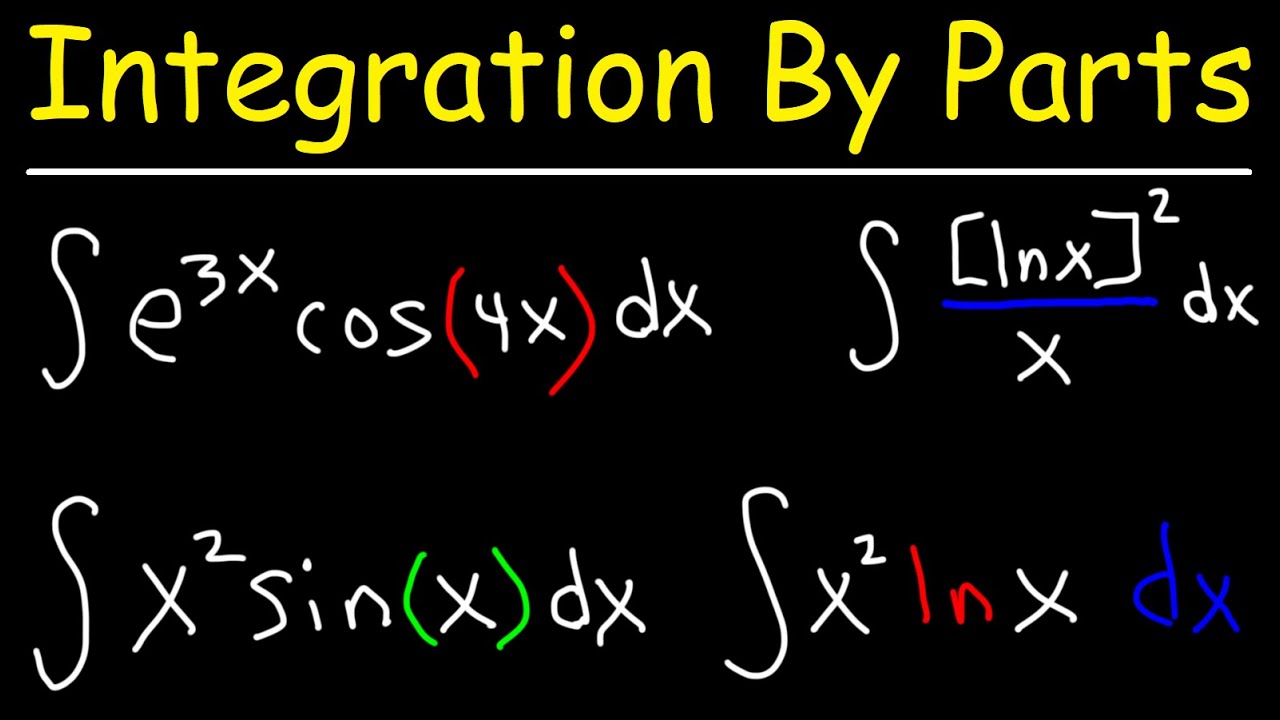Introduction and Definition of integration by parts

Introduction

Introduction:

Integration by parts is a powerful technique used in calculus to find the integral of a product of two functions. It is a method of breaking down complex integrals into simpler ones, often resulting in a reduction of the overall complexity of the problem.

The technique is based on the product rule from differentiation, which states that the derivative of a product of two functions is equal to the derivative of the first function multiplied by the second function, plus the first function multiplied by the derivative of the second function.

Integration by parts reverses this process by expressing the derivative of a product of two functions as the product of one function with the integral of the other function, plus the integral of the first function multiplied by the derivative of the other function. This allows us to solve integrals that would otherwise be difficult or impossible to evaluate using basic integration rules.

Integration by parts is particularly useful when dealing with integrals involving algebraic functions, logarithmic functions, trigonometric functions, and exponential functions. It is a fundamental technique in the field of calculus and is commonly used to solve a wide range of problems in physics, engineering, economics, and other scientific disciplines.

By applying this technique, we are able to evaluate a wide range of integrals that might initially seem daunting or impossible to solve.

Definition of integration by parts

Integration by parts is a technique used in calculus to evaluate the integral of a product of two functions. It is derived from the product rule of differentiation.

The formula for integration by parts is given as follows:

∫u(x)v'(x)dx = u(x)v(x) – ∫v(x)u'(x)dx

In this formula, u(x) and v(x) are two functions of x, and u'(x) and v'(x) represent their respective derivatives with respect to x.

Integration by parts allows one to transform an integral from one form to another, which may be easier to evaluate. It is typically used when the integral involves a product of functions that cannot be directly integrated by other standard techniques, such as substitution or trigonometric identities.

The choice of u(x) and v'(x) in the formula is crucial to simplify the integral. Usually, u(x) is chosen as a function that becomes simpler after taking its derivative, while v'(x) is chosen as the derivative of a function that can be easily integrated.

Integration by parts is a powerful tool in calculus, often employed when dealing with more complicated functions and in various areas of mathematics and physics, such as finding areas under curves, evaluating certain types of improper integrals, and solving differential equations.

How integration by parts works

Integration by parts is a technique used in calculus to find the integral of a product of two functions. It is based on the product rule from differentiation. The general formula for integration by parts is:

∫u dv = uv – ∫v du

In this formula, u and v are functions, and du and dv are their differentials. The technique involves choosing u and dv in a way that simplifies the integral on the right-hand side of the equation.

To apply integration by parts, we follow these steps:

1. Choose a function u to differentiate. This function should be chosen based on a priority order called “LIATE” (Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential). The function that appears earlier in the LIATE order should be chosen as u.

2. Differentiate u to find du.

3. Choose a function dv to integrate. This function should be chosen in a way that its integral can be easily computed.

4. Integrate dv to find v.

5. Use the integration by parts formula to rewrite the original integral in terms of u, v, du, and dv.

6. Simplify the integral obtained on the right-hand side of the formula.

7. If necessary, repeat the process by choosing another pair of u and dv and integrating further until the integral is fully evaluated.

Integration by parts is particularly useful when the integral involves products of functions that are difficult to integrate using other techniques. It allows us to transform the original integral into a simpler form that can be easily evaluated. However, it is important to note that integration by parts may require multiple iterations or additional manipulation to obtain a final result.

Examples of integration by parts

1) Example 1:

Let’s consider the integral of x * cos(x) dx.

To solve this integral, we can use integration by parts.

We choose u = x and dv = cos(x) dx.

Taking the derivatives, du = dx and v = sin(x).

Now, using the formula for integration by parts:

∫ x * cos(x) dx = x * sin(x) – ∫ sin(x) dx

= x * sin(x) + cos(x) + C

where C is the constant of integration.

2) Example 2:

Let’s find the integral of ln(x) dx.

To solve this integral, we can use integration by parts.

We choose u = ln(x) and dv = dx.

Taking the derivatives, du = (1/x) dx and v = x.

Now, using the formula for integration by parts:

∫ ln(x) dx = x * ln(x) – ∫ (1/x) * x dx

= x * ln(x) – ∫ dx

= x * ln(x) – x + C

where C is the constant of integration.

3) Example 3:

Let’s evaluate the integral of e^x * sin(x) dx.

To solve this integral, we can use integration by parts.

We choose u = e^x and dv = sin(x) dx.

Taking the derivatives, du = e^x dx and v = -cos(x).

Now, using the formula for integration by parts:

∫ e^x * sin(x) dx = -e^x * cos(x) – ∫ (-cos(x)) * e^x dx

= -e^x * cos(x) + ∫ e^x * cos(x) dx

Now, we have a similar integral on both sides. So, we can solve for it.

2 * ∫ e^x * sin(x) dx = -e^x * cos(x)

∫ e^x * sin(x) dx = (-1/2) * e^x * cos(x) + C

where C is the constant of integration.

Conclusion

In conclusion, integration by parts is a useful technique in calculus that allows us to simplify the integration of a product of two functions. It is based on the product rule of differentiation and can help us solve integrals that would otherwise be difficult or impossible to evaluate.

The integration by parts formula is given by:

∫ u dv = uv – ∫ v du

Where u and v are functions of x, and du and dv are their respective differentials.

By choosing appropriate u and dv, we can often simplify the integral and make it easier to evaluate. The goal is to choose u and dv in such a way that the new integral on the right-hand side is simpler than the original one.

Integration by parts is especially useful when dealing with functions that cannot be integrated algebraically or when faced with indefinite integrals that involve logarithmic, exponential, or trigonometric functions.

Overall, integration by parts is a powerful tool that allows us to find antiderivatives and solve a wide range of integration problems. It is an important technique to master in calculus and can be used in various applications across mathematics and science.

Topics related to Integration by parts