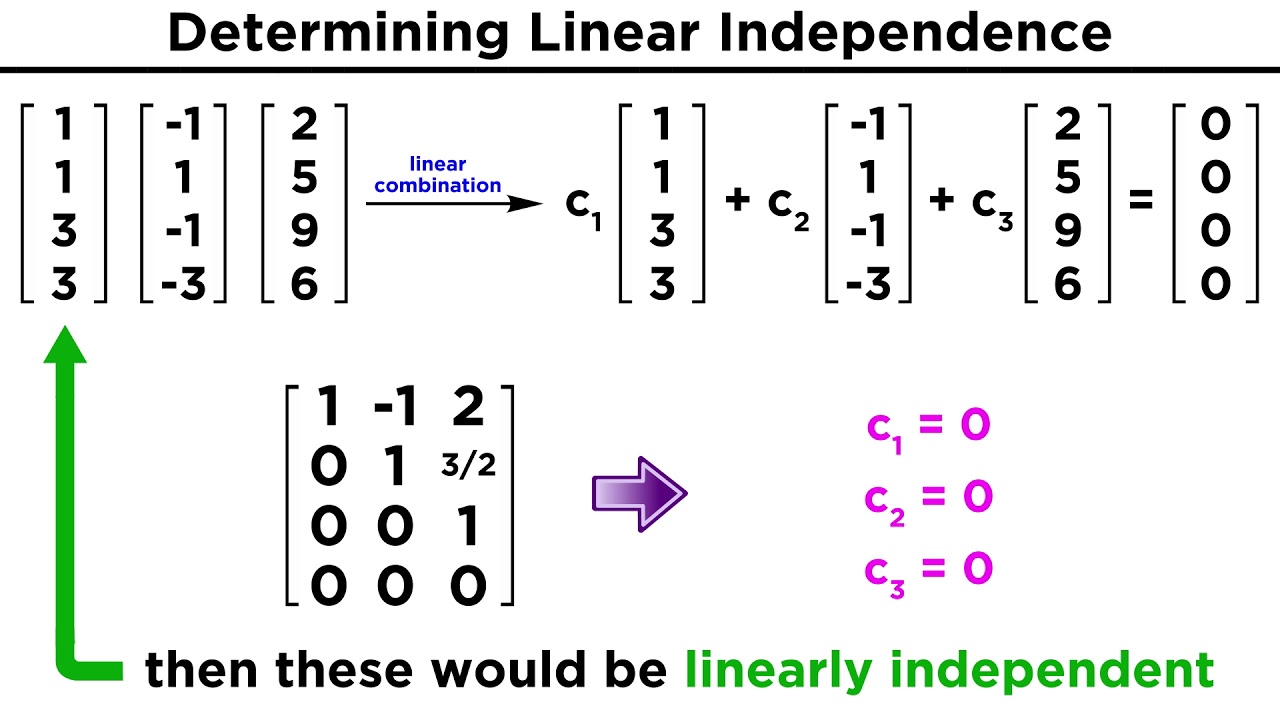
Introduction and Definition of linear dependence

Introduction

Introduction:

Linearly dependent refers to a concept in linear algebra that describes a set of vectors that can be written as a linear combination of each other. In other words, if we have a set of vectors and one of them can be expressed as a linear combination of the others, then the set is said to be linearly dependent.

Explanation of Linearly Dependent:

To understand linearly dependent sets, it is important to understand what a linear combination of vectors means. A linear combination of vectors is formed by multiplying each vector by a scalar (a real number) and adding the results. For example, if we have two vectors, v1 and v2, their linear combination would be αv1 + βv2, where α and β are scalars.

Now, let’s consider a set of vectors {v1, v2, v3, …, vn}. This set is said to be linearly dependent if there exist scalars α1, α2, α3, …, αn, not all zero, such that α1v1 + α2v2 + α3v3 + … + αnvn = 0, where 0 is the zero vector. In other words, if a non-trivial solution (i.e., a solution where not all scalars are zero) exists for this equation, the set is linearly dependent.

In practical terms, linear dependence means that one or more vectors in the set can be expressed as a linear combination of the other vectors in the set. For example, if v2 = 2v1, then the set {v1, v2} is linearly dependent because v2 can be obtained by scaling v1.

Importance of Linearly Dependent Sets:

Understanding linearly dependent sets is important in linear algebra because they have certain properties and implications. For instance, a linearly dependent set cannot form a basis for a vector space, as a basis requires linear independence. Linearly dependent sets also have a non-trivial null space and can lead to redundancy in systems of linear equations. Therefore, recognizing linear dependence helps in simplifying calculations, reducing complexity, and identifying important vectors in a given set.

Conclusion:

In conclusion, linearly dependent sets are sets of vectors that can be expressed as a linear combination of each other. This concept is important in linear algebra as it helps in understanding vector spaces, systems of linear equations, and essential properties of vectors. Recognizing linear dependence allows for simplification and a deeper understanding of the relationships between vectors.

Definition of linear dependence

Linear dependence refers to a mathematical relationship between a set of vectors in a vector space. In this context, a set of vectors is said to be linearly dependent if one or more vectors in the set can be expressed as a linear combination of the other vectors in the set.

More formally, a set of vectors {v₁, v₂, …, vₙ} is linearly dependent if there exist scalars c₁, c₂, …, cₙ (not all equal to zero) such that the linear combination c₁v₁ + c₂v₂ + … + cₙvₙ equals the zero vector.

Linear dependency implies that at least one vector in the set can be eliminated without losing any information, as it can be represented by a combination of the remaining vectors.

On the other hand, a set of vectors is said to be linearly independent if no vector in the set can be expressed as a linear combination of the other vectors. In other words, all the vectors in a linearly independent set are essential and cannot be eliminated without resulting in a loss of information.

Properties and examples

A set of vectors in a vector space is said to be linearly dependent if at least one vector in the set can be defined as a linear combination of the other vectors.

A property of linearly dependent vectors is that one or more of the vectors can be expressed as a linear combination of the remaining vectors. In other words, if a set of vectors {v1, v2, …, vn} is linearly dependent, there exist scalars c1, c2, …, cn (not all zero) such that:

c1v1 + c2v2 + … + cnvn = 0

Some examples of linearly dependent vectors include:

1. In R^2 (two-dimensional Euclidean space), consider the vectors v1 = [1, 2] and v2 = [2, 4]. Since v2 is simply twice v1, these vectors are linearly dependent.

2. In R^3 (three-dimensional Euclidean space), consider the vectors v1 = [1, 2, 3], v2 = [2, 4, 6], and v3 = [3, 6, 9]. Here, v3 can be expressed as the sum of v1 and v2 (v3 = v1 + v2), making these vectors linearly dependent.

3. In the vector space of polynomials, consider the vectors v1(x) = x^2, v2(x) = 2x^2, and v3(x) = 3x^2. Since v2 is twice v1 and v3 is three times v1, these polynomials are linearly dependent.

Overall, if any vector in a set can be expressed as a linear combination of the other vectors in the set, those vectors are linearly dependent.

Linear dependence in vectors

In linear algebra, linear dependence refers to a condition where a set of vectors is not linearly independent. In other words, one or more vectors in the set can be expressed as a linear combination of the other vectors.

To determine if a set of vectors is linearly dependent, we can check if there exist non-zero coefficients such that the linear combination of the vectors equals the zero vector. If such coefficients exist, it implies that the vectors are linearly dependent.

For example, let’s consider a set of vectors:

V1 = (1, 2, 3)

V2 = (-1, -2, -3)

V3 = (2, 4, 6)

We can check if these vectors are linearly dependent by solving the equation:

c1*V1 + c2*V2 + c3*V3 = 0, where c1, c2, and c3 are coefficients.

Substituting the given vectors, we have:

c1*(1, 2, 3) + c2*(-1, -2, -3) + c3*(2, 4, 6) = (0, 0, 0)

Simplifying, we get the following system of equations:

c1 – c2 + 2c3 = 0

2c1 – 2c2 + 4c3 = 0

3c1 – 3c2 + 6c3 = 0

By solving this system of equations, we find that c1 = -c2 = c3. This implies that the set of vectors is linearly dependent since we can express any vector in terms of the other vectors.

Linearly dependent vectors can be thought of as redundant or having overlapping information. They do not provide additional information beyond what can be obtained from a subset of the vectors.

In practical terms, linear dependence can cause issues in mathematical calculations and applications. In linear systems, it can lead to infinite solutions or an inability to uniquely solve the system. It is often desirable to work with linearly independent vectors to ensure computational stability and meaningful results.

Significance in mathematical applications

In mathematical applications, linear dependence refers to the relationship between vectors in a vector space. Specifically, a set of vectors is said to be linearly dependent if one or more of the vectors in the set can be expressed as a linear combination of the others.

Understanding linear dependence is significant in various mathematical fields and applications. Here are a few examples:

1. Determining Basis: Linearly dependent vectors cannot form a basis for a vector space because they introduce redundancy. Therefore, identifying linear dependence is crucial in finding a basis, which is a fundamental concept in linear algebra.

2. Solving Systems of Equations: Linear dependence plays a role in solving systems of linear equations. If a system has linearly dependent equations, then some information is redundant, and the system may have infinitely many solutions.

3. Dimension of Vector Spaces: Linear dependence helps determine the dimension of a vector space, which is the number of linearly independent vectors required to span the space. Linear dependence can reduce the dimension by showing that certain vectors can be represented as combinations of others.

4. Eigenvalues and Eigenvectors: Linear dependence is important in the study of eigenvalues and eigenvectors. Linearly dependent eigenvectors can indicate that the matrix has repeated eigenvalues and corresponds to a certain geometric transformation.

5. Data Analysis: In data analysis, linear independence is essential for assessing the relationship between variables. Linearly dependent variables in a dataset can lead to multicollinearity issues, making it difficult to interpret and analyze the data accurately.

Overall, understanding linear dependence is significant in various mathematical applications, providing insights into fundamental concepts such as basis, dimension, solution uniqueness, and relationships between variables.

Topics related to Linearly dependent