Introduction to Chords in Mathematics and Definition and Properties of Chords

Introduction to Chords in Mathematics

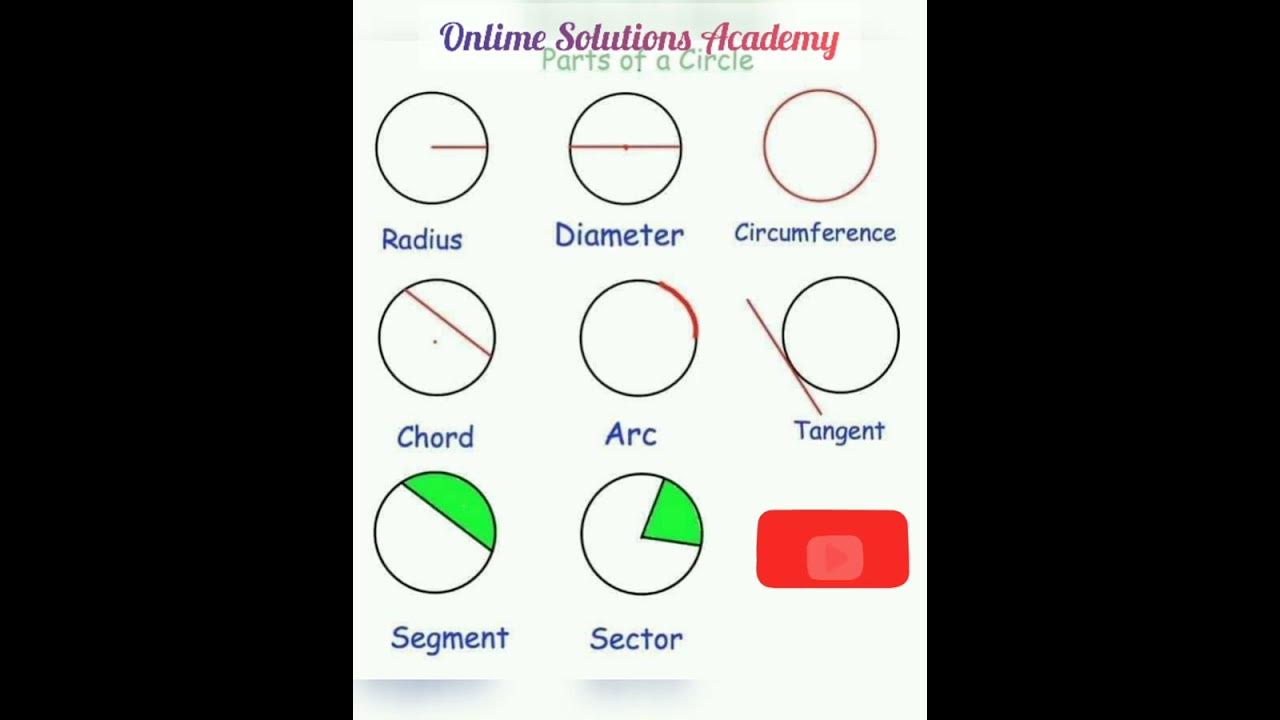
In mathematics, a chord refers to a line segment that connects two points on a curve. When it comes to studying chords in mathematics, we often focus on chords in the context of circles. A circle is a geometric figure in which every point on the curve is equidistant from a fixed point called the center.

In the case of a circle, a chord can be drawn by selecting any two points on the circle and connecting them with a straight line. The chord can be either a line that passes through the center of the circle, called the diameter, or a line that doesn’t pass through the center, called a minor chord. A chord that passes through the center is also called a major chord.

Chords have several important properties and relationships in mathematics:

1. Length: The length of a chord can be determined by measuring the distance between its endpoints. This can be done using the Pythagorean theorem or other distance formulas.

2. Perpendicular Bisector: The perpendicular bisector of a chord is a line that divides the chord into two equal halves, while being perpendicular to the chord. The intersection point of the perpendicular bisector with the chord is always the midpoint of the chord.

3. Central Angle: The central angle of a chord is the angle formed at the center of the circle by two radii that connect the center to the endpoints of the chord. The measure of the central angle is equal to twice the measure of the inscribed angle that intercepts the same arc as the chord.

4. Inscribed Angle: The inscribed angle of a chord is the angle formed by two radii that connect the center to an endpoint of the chord. The measure of the inscribed angle is half the measure of the central angle that intercepts the same arc as the chord.

5. Intersecting Chords Theorem: If two chords intersect inside a circle, the products of the segments they create are equal. Specifically, the product of the segments of one chord is equal to the product of the segments of the other chord.

Chords in mathematics are important in various applications, such as geometry, trigonometry, and calculus. They have numerous properties that help us analyze and solve problems involving circles. Understanding the properties and relationships of chords is crucial for solving mathematical problems involving circles and other curved shapes.

Definition and Properties of Chords

A chord in music refers to a group of three or more pitches played simultaneously to create harmony. It is formed by combining multiple notes from a given scale, usually stacked in thirds. The root note of the chord determines its name, and the other notes are called the chord’s intervals or degrees.

Some key properties of chords include:

1. Pitch: Chords are composed of specific pitches or notes. The specific combination of these pitches determines the quality and character of the chord.

2. Harmony: Chords create harmony by combining different pitches that complement each other, resulting in a pleasing sound when played together.

3. Tonal Center: Chords are usually built around a specific tonal center or key. The root note of the chord often serves as the tonal center and provides the overall sense of tonality in a musical composition.

4. Tension and Resolution: Chords can create tension by using dissonant intervals, which are intervals that sound unstable or clash with each other. The resolution occurs when these intervals are resolved into consonant intervals, which sound stable and harmonious.

5. Chord Progressions: Chords are typically used in progressions, where a series of chords are played in a specific order to create a musical structure or form. Chord progressions are fundamental to creating melody and structure in music.

6. Inversions: Chords can be inverted by changing the order of the notes within the chord. Inversions can give a different voicing to the chord while still maintaining its basic structure and harmony.

Overall, chords form the foundation of harmony in music and are essential for creating a diverse range of tonal and emotional effects.

Application of Chords in Geometry

Chords in geometry are an important element in various applications. A chord is a line segment that connects two points on a circle. They can be used to solve problems and determine important properties of circles and other geometric shapes.

One application of chords is in the calculation of the length of a circle. The length of a chord can be used, along with the radius of the circle, to find the circumference of the circle. This can be done using the formula C = πd, where C is the circumference, and d is the diameter of the circle. Since a chord can be considered as a diameter passing through a point, measuring the chord and doubling it can give the diameter, enabling the calculation of the circumference.

Chords also play a significant role in the properties of tangents and secants. A tangent line is a line that touches a circle at only one point, while a secant line intersects the circle at two points, one of which could be the endpoints of a chord. By studying the lengths and angles formed by these lines and chords, geometric theorems such as the chord-chord theorem and the angle in the semicircle can be derived.

Additionally, chords are essential in determining the position of a point relative to a circle. For example, the perpendicular bisector of a chord passes through the center of the circle. This property allows the construction of the center of a circle using just a compass and a straightedge.

Moreover, chords are used in the design and construction of various structures. In architecture, particularly when creating arches, chords are used to determine the shape and dimensions of the arch. By using multiple chords, an arch can be accurately constructed and ensure stability.

In summary, chords in geometry have numerous applications, including calculating the circumference of a circle, determining the properties of tangents and secants, locating the center of a circle, and constructing arches. Understanding the properties and characteristics of chords is fundamental in solving geometrical problems and designing structures.

Importance of Chords in Trigonometry

Chords play a crucial role in trigonometry as they help define and calculate various important geometric properties and relationships within a circle.

In trigonometry, a chord is a line segment that joins two points on the circumference of a circle. It can be any line segment that connects two points on the circle, whether it passes through the center of the circle (diameter) or not.

One of the key concepts of trigonometry is the unit circle, which is a circle with a radius of 1 unit. Chords on the unit circle help define the values of trigonometric functions such as sine, cosine, and tangent.

Using chords, we can determine the lengths of arcs and angles in a circle. The length of an arc between two points on a circle is directly proportional to the measure of the central angle subtended by the arc. Knowing the length of a chord and the radius of the circle, we can calculate the measure of the corresponding central angle using the formula:

θ = 2 * arcsin (c / 2r)

where θ is the central angle, c is the length of the chord, and r is the radius of the circle.

Chords also help in calculating the area of a circular segment, which is the region bounded by a chord and the arc of the circle intercepted by the chord. By knowing the length of the chord and the distance from the center of the circle to the chord (perpendicular distance), we can calculate the area of the segment.

Moreover, chords are essential in trigonometric identities and equations. For example, the Pythagorean identity, which relates the sine and cosine functions, can be derived by considering a right-angled triangle inscribed within a circle and using the lengths of the chords.

In summary, chords are significant in trigonometry as they help determine angles, arcs, areas, and establish various relationships within a circle. They form the basis for many trigonometric calculations and concepts, making them a fundamental element in trigonometry.

Examples and Practice Problems Involving Chords

Example 1:

Consider a circle with a radius of 7 units. If a chord is drawn within the circle and its length is 10 units, what is the distance from the center of the circle to the chord?

Solution:

To solve this problem, we can draw a radius from the center of the circle to one of the endpoints of the chord. This radius will be perpendicular to the chord and will bisect it.

Using the properties of right triangles, we can create a right triangle with one leg being the radius (7 units) and the hypotenuse being half of the chord length (5 units).

Applying the Pythagorean theorem, we can find the other leg of the right triangle, which represents the distance from the center of the circle to the chord:

Distance^2 + 7^2 = 5^2

Distance^2 = 25 – 49

Distance^2 = -24

Since the square of a distance cannot be negative, we can conclude that there is no distance between the center of the circle and the chord. In other words, the center of the circle lies on the chord.

Example 2:

In a circle with a radius of 8 units, a chord is drawn. The length of this chord is 12 units. Find the distance between the center of the circle and the chord.

Solution:

Similar to the previous example, we can draw a radius from the center of the circle to one of the endpoints of the chord. Since the chord length is greater than the radius, the radius will bisect the chord and be shorter than the height of the triangle formed by the chord and the radius.

Using the Pythagorean theorem, we can find the distance from the center of the circle to the chord:

Distance^2 + 8^2 = (12/2)^2

Distance^2 + 64 = 36

Distance^2 = 36 – 64

Distance^2 = -28

Again, the square of a distance cannot be negative, so we can conclude that there is no distance between the center of the circle and the chord. The center of the circle lies on the chord.

Topics related to Chord