Introduction to Markov Process and Definition of a Markov Process

Introduction to Markov Process

Markov Process is a mathematical framework used to model systems that exhibit random behavior over time. It is named after the Russian mathematician Andrey Markov, who introduced the concept in the early 20th century.

In a Markov Process, the future state of the system depends only on its current state and is independent of its past states. This property is known as the Markov property or the memoryless property. It implies that the system has no memory of how it reached its current state, and all relevant information is encapsulated in the current state alone.

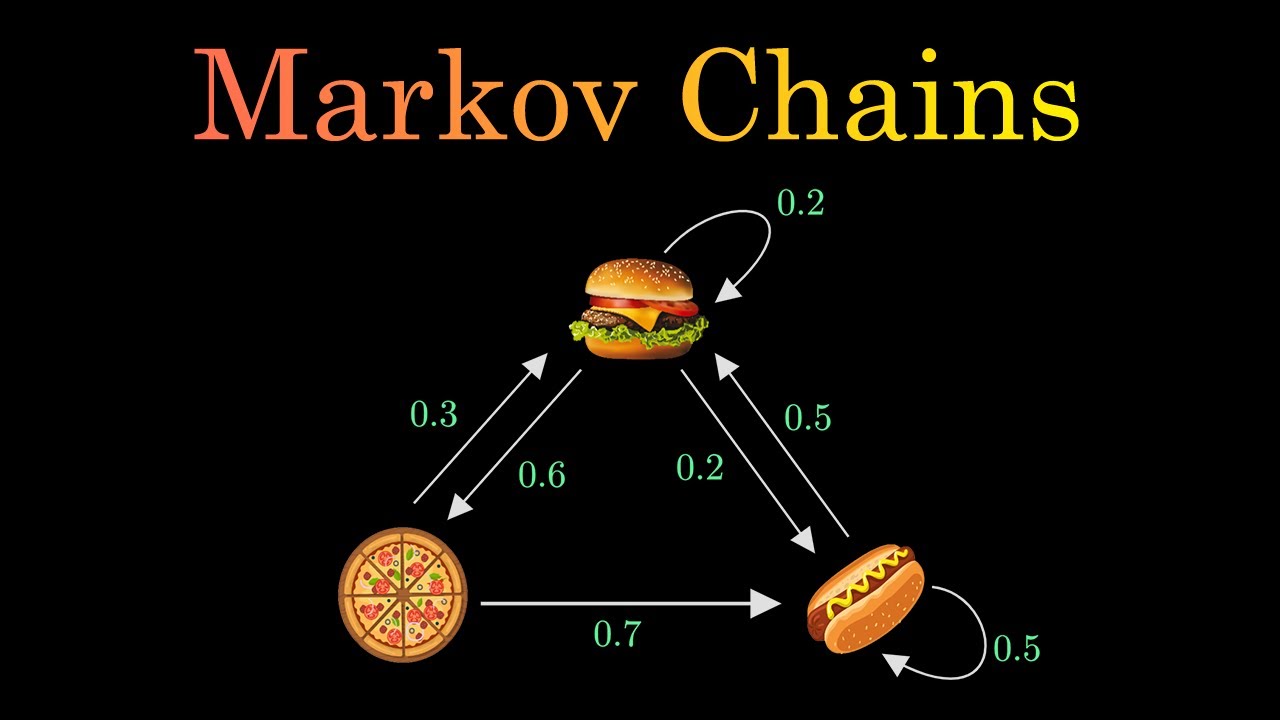
A Markov Process can be represented mathematically as a collection of states and a set of transition probabilities between those states. Each state represents a possible situation of the system, and the transition probabilities define the likelihood of moving from one state to another.

The process evolves in discrete time, where at each time step, the system transitions to a new state according to the specified transition probabilities. The sequence of states and their corresponding probabilities form a trajectory or path of the process.

Various real-world phenomena can be modeled using Markov Processes, such as stock price movements, weather patterns, population dynamics, and even language generation in natural language processing systems. Markov Processes provide a powerful tool to analyze and predict the behavior of such systems, based on the underlying transition probabilities.

Important concepts related to Markov Processes include the state space, which is the set of all possible states of the system, and the transition matrix, which contains the transition probabilities between states. Markov Processes can also be classified into different types based on their properties, such as discrete-time or continuous-time processes, stationary or non-stationary processes, and homogeneous or non-homogeneous processes.

Overall, Markov Processes serve as a fundamental framework for understanding and modeling random systems, allowing us to make predictions and draw insights about their future behavior based on their current state.

Definition of a Markov Process

A Markov process, also known as a Markov chain, is a mathematical model that describes a sequence of events or states where the probability of transitioning from one state to another depends only on the current state and is independent of the past.

In a Markov process, the system is assumed to be in a discrete set of states, and the transition probabilities between states are defined by a transition matrix. This matrix represents the probabilities of moving from one state to another within a single time step.

The Markov property states that the future behavior of the process is only influenced by the current state and not by any previous states. This property is also referred to as memorylessness.

Markov processes are widely used in various fields, including physics, economics, computer science, and finance, to model and analyze systems that exhibit stochastic behavior or random transitions between states. They provide a tool to study the statistical properties and long-term behavior of such systems.

Properties of Markov Processes

A Markov process, also known as a Markov chain, is a stochastic process that satisfies the Markov property. The Markov property states that the conditional probability distribution of future states only depends on the current state and is independent of the past states.

Some properties of Markov processes include:

1. Memorylessness: A Markov process has no memory. This means that the future behavior of the process only depends on the current state and is independent of the path taken to reach that state. The process does not remember or take into account any historical information.

2. State space: A Markov process operates in a defined state space, which is a set of all possible states that the process can be in. The state space can be finite or infinite.

3. Transition probabilities: A Markov process is characterized by the transition probabilities between states. The transition probability is the likelihood of moving from one state to another in a single time step. These probabilities are typically represented by a transition matrix or transition diagram.

4. Stationarity: A Markov process can be stationary, meaning that the transition probabilities between states remain constant over time. This property allows for the long-term behavior of the process to be analyzed and predicted.

5. Markov property: The key property of a Markov process is that future states are conditionally independent of past states given the current state. This property allows for efficient computation and modeling of the process.

6. Ergodicity: If a Markov process is ergodic, it means that it is irreducible (there are no unreachable states) and aperiodic (the process does not have a predictable pattern). Ergodicity ensures that the process will eventually visit all states and that the long-term behavior can be characterized by a stationary distribution.

These properties make Markov processes widely used in various fields such as statistics, economics, physics, and computer science. They are particularly useful for modeling and analyzing systems that exhibit random behavior over time.

Applications of Markov Processes

Markov processes, also known as Markov chains, are mathematical models that describe the probability of transitioning between different states over time. They have a wide range of applications in various fields, including:

1. Finance: Markov processes are used in finance to model stock prices, interest rates, and exchange rates. They can help estimate future probabilities and predict market trends.

2. Biology: Markov processes are employed to model biological processes such as gene regulatory networks, protein folding, and population dynamics. They can provide insights into the behavior and evolution of biological systems.

3. Queueing theory: Markov processes are used to model queueing systems, such as customer queues in call centers or traffic flow in transportation networks. They can help optimize resource allocation and improve efficiency.

4. Machine Learning: Markov processes are used in various machine learning algorithms, such as Hidden Markov Models (HMMs) and Markov Decision Processes (MDPs). HMMs are used for tasks like speech recognition and language modeling, while MDPs are used for reinforcement learning problems.

5. Natural Language Processing: Markov processes are used in language modeling tasks, such as speech recognition, machine translation, and text generation. They can help predict the probability of a word given its context.

6. Physics: Markov processes are used in physics to model a wide range of phenomena, including diffusion processes, random walks, and thermodynamics. They can provide insights into the behavior of complex systems.

7. Operations Research: Markov processes are used in operations research to model and analyze stochastic systems, such as inventory management, production systems, and supply chains. They can help optimize decision-making and resource allocation.

8. Epidemiology: Markov processes are used to model the spread of diseases, such as contagious infections, and predict the future course of an epidemic. They can assist in designing effective control strategies and understanding the impact of interventions.

Markov processes have many other applications across various disciplines. Their ability to model and analyze systems with probabilistic transitions between states makes them a powerful tool for understanding and predicting complex phenomena.

Conclusion

In conclusion, Markov process is a mathematical model that describes a sequence of events where the probability of transitioning to the next event depends only on the current state. It is a stochastic process that has wide applications in various fields, including economics, physics, biology, and computer science.

One of the key features of a Markov process is the Markov property, which states that the future events are independent of the past given the current state. This property allows for efficient calculations and predictions based on the current state. Markov processes are often represented as a set of states and a transition matrix that specifies the probabilities of transitioning between states.

Markov processes can be classified into different types, depending on the characteristics of the state space and transitions. Some common types include discrete-time Markov chains, continuous-time Markov chains, and hidden Markov models.

Markov processes have numerous practical applications. For example, they can be used to model the movement of molecules in a chemical reaction, the fluctuations of stock prices in financial markets, the behavior of customers in a queueing system, or the evolution of language in natural language processing.

In summary, Markov processes are powerful mathematical tools for modeling and analyzing various systems that exhibit random behavior. They provide a probabilistic framework for understanding and predicting future events based on current states, making them valuable in a wide range of fields.

Topics related to Markov Process