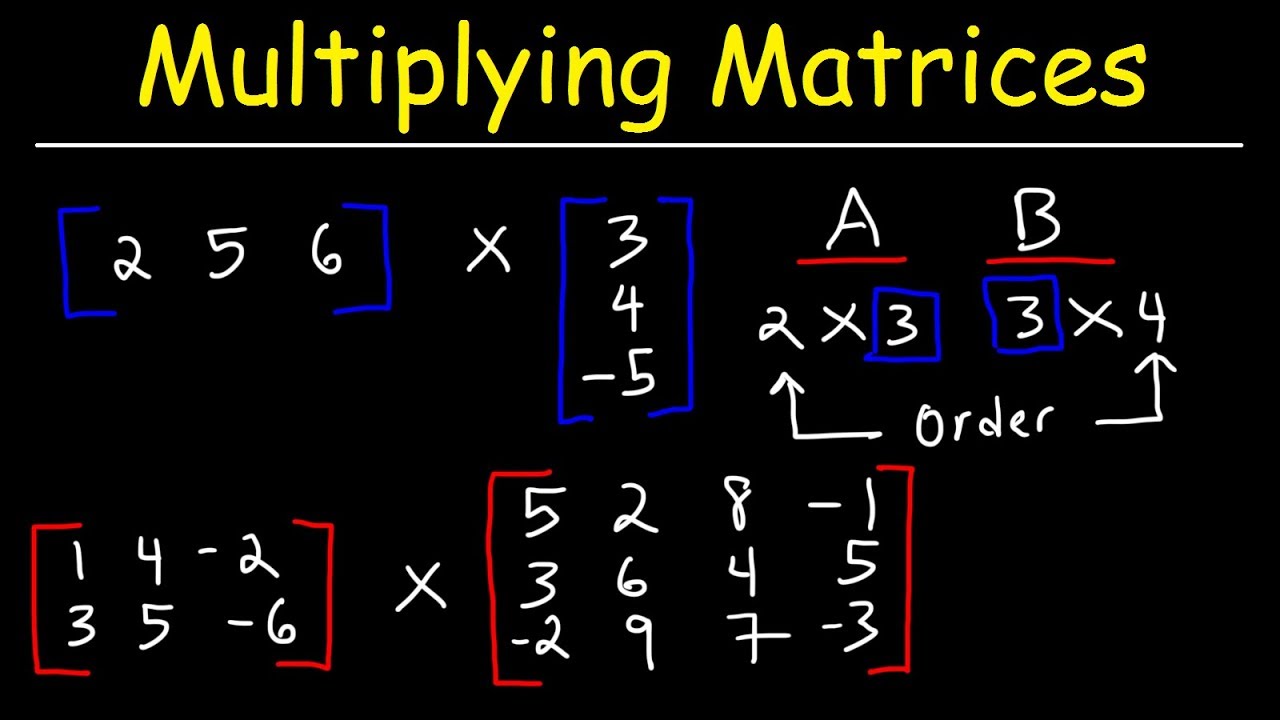
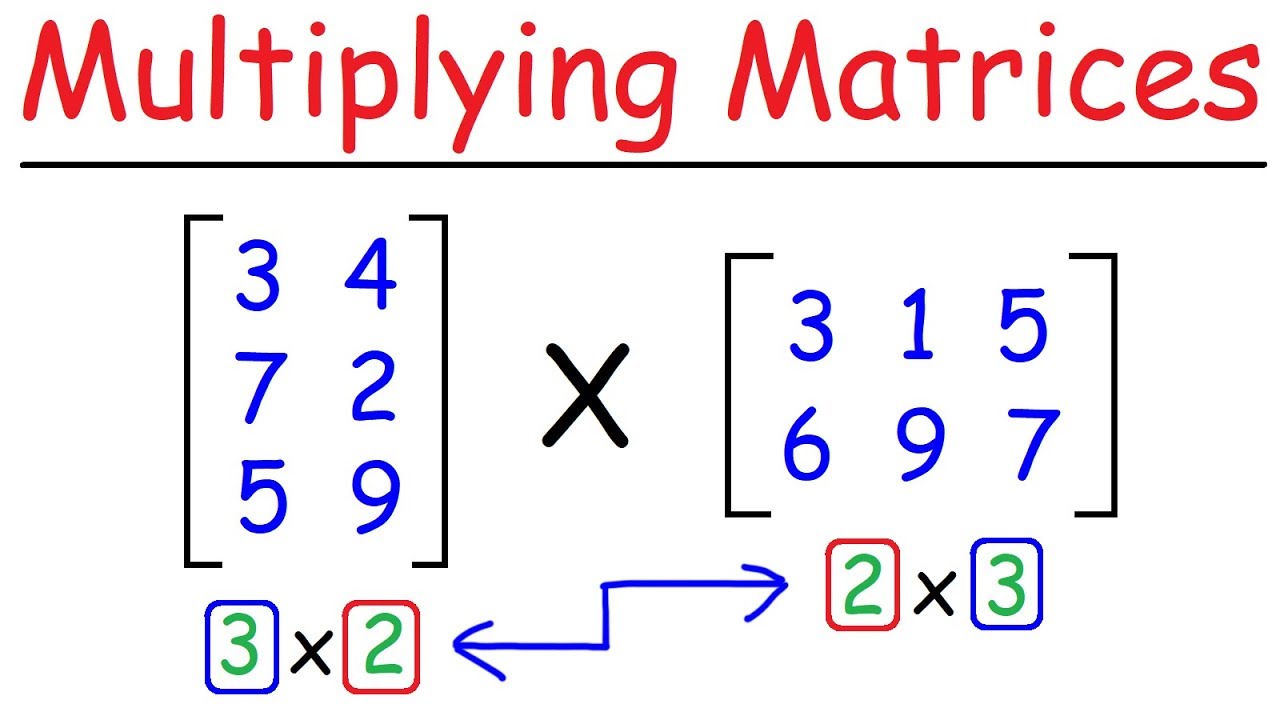
Introduction to Matrix multiplication and Definition of Matrix multiplication

Introduction to Matrix multiplication

Matrix multiplication is a fundamental operation in linear algebra that involves multiplying two matrices to produce a new matrix. It is a mathematical process that combines the elements of one matrix with the elements of another matrix to generate a resulting matrix.

In order for matrix multiplication to be defined, the number of columns in the first matrix must equal the number of rows in the second matrix. The resulting matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.

To compute the elements of the resulting matrix, the row elements of the first matrix are multiplied with the corresponding column elements of the second matrix, and these products are then summed up. This process is performed for each element of the resulting matrix.

Matrix multiplication is not commutative, meaning that the order in which the matrices are multiplied is significant. In general, AB is not equal to BA. Therefore, it is important to ensure that the matrices are arranged in the correct order for multiplication.

Matrix multiplication has various applications, including solving systems of linear equations, transforming geometric objects, and representing linear transformations. It is a fundamental operation in many fields of mathematics, physics, engineering, and computer science.

Overall, matrix multiplication is a powerful tool that allows for the manipulation and combination of matrices, enabling a wide range of mathematical and computational operations.

Definition of Matrix multiplication

Matrix multiplication is a binary operation that is performed on two matrices to produce a new matrix. It involves multiplying the individual elements of the matrices and then summing up the products in a specific way to obtain the resulting matrix.

The process of matrix multiplication follows certain rules:

1. The number of columns in the first matrix must be equal to the number of rows in the second matrix.

2. For each element in the resulting matrix, the value is obtained by multiplying the corresponding row of the first matrix with the corresponding column of the second matrix, and then summing up the products.

3. The resulting matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.

Matrix multiplication is not commutative, which means that the order of the matrices does matter. In other words, multiplying matrix A by matrix B will produce a different result than multiplying matrix B by matrix A.

Properties of Matrix multiplication

Matrix multiplication is an operation that combines two matrices to produce a new matrix. It is important to note that matrix multiplication is not commutative, meaning that AB is not equal to BA in general unless some special conditions are met.

Here are some key properties of matrix multiplication:

1. Closure: Matrix multiplication is closed, which means that the product of two matrices is always another matrix.

2. Associativity: Matrix multiplication is associative, meaning that (AB)C = A(BC) for all compatible matrices A, B, and C.

3. Distributivity: Matrix multiplication distributes over matrix addition, which means that A(B + C) = AB + AC for all compatible matrices A, B, and C.

4. Identity Element: The identity matrix serves as the identity element for matrix multiplication. If I is the identity matrix of appropriate size, then AI = IA = A for any compatible matrix A.

5. Zero Element: The zero matrix acts as a zero element for matrix multiplication. If O is the zero matrix of appropriate size, then AO = OA = O for any compatible matrix A.

6. Different dimensions: The dimensions of the matrices involved in matrix multiplication must satisfy a compatibility condition. Specifically, if A is m×n and B is n×p, the resulting product AB will have dimensions m×p.

7. Non-commutativity: In general, matrix multiplication is not commutative. This means that AB and BA can be different matrices, except in special cases such as when A and B are both square matrices and one of them is the identity matrix.

8. Determinant of product: The determinant of a product of matrices is equal to the product of their determinants, i.e., det(AB) = det(A) * det(B).

These properties help us understand and manipulate matrices using matrix multiplication, making it a key operation in linear algebra and many other fields of mathematics and sciences.

Methods for performing Matrix multiplication

There are several methods for performing matrix multiplication. Here are a few common methods:

1. Row by column multiplication: In this method, you multiply each element in a row of the first matrix by the corresponding element in a column of the second matrix, and then sum up these products to get the resulting element in the output matrix. Repeat this process for each element in the output matrix.

2. Dot product method: This method is an extension of the row by column multiplication. In this method, you take the dot product of each row in the first matrix with each column in the second matrix to obtain the elements of the output matrix.

3. Block matrix multiplication: This method involves dividing the matrices into smaller sub-matrices called blocks and performing multiplication of these blocks. The resulting blocks are then combined to form the output matrix.

4. Strassen’s algorithm: Strassen’s algorithm is an efficient divide-and-conquer method for matrix multiplication. It recursively divides the matrices into smaller sub-matrices, performs multiplication using these sub-matrices, and then combines the results to obtain the final output matrix.

5. Parallel algorithms: Matrix multiplication can also be performed in parallel using multiple processors or computing units. Various parallel algorithms such as Cannon’s algorithm, Fox’s algorithm, and others can be used to distribute and compute the matrix elements simultaneously.

These are just a few methods for performing matrix multiplication. The choice of method depends on factors such as the size of the matrices, computational resources available, and the desired efficiency or speed of computation.

Applications of Matrix multiplication

Matrix multiplication is a fundamental operation in linear algebra with several important applications. Here are some of the key applications of matrix multiplication:

1. Transformations: Matrix multiplication is commonly used to represent transformations in different coordinate systems. For example, in computer graphics, matrices are used to scale, rotate, and translate objects in 2D and 3D space. Each transformation is encoded as a matrix, and to apply multiple transformations in sequence, matrix multiplication is performed.

2. Systems of Linear Equations: Matrix multiplication is used to solve systems of linear equations. Given a system of equations in matrix form (Ax=b), where A is a coefficient matrix, x is the variable matrix, and b is the solution matrix, multiplying both sides by the inverse of A allows us to solve for x. Matrix multiplication is crucial in performing this inverse operation.

3. Markov Chains: Markov chains are stochastic models used to analyze random processes. They can be represented as a series of transition matrices, each representing the probabilities of transitioning from one state to another. To calculate the long-term behavior of a Markov chain, matrix multiplication is employed, with the transition matrices raised to a power, representing the number of transitions.

4. Graph Theory: Matrices can be used to represent graphs, where each element of the matrix represents the presence or absence of an edge between two vertices. Matrix multiplication can then be used to determine paths, cycles, and connectivity between different vertices in a graph.

5. Image Processing: Matrix operations, including matrix multiplication, are extensively used in image processing techniques such as Fourier transformations, image compression, and image filtering. These operations involve manipulating the pixel values of an image using matrix operations to achieve desired effects.

6. Neural Networks: Matrix multiplication is a core component in training and inference of neural networks. In a neural network, each layer’s output is computed by multiplying the input matrix (representing the activations) with a weight matrix, and applying an activation function. These operations are repeated layer by layer through matrix multiplication, allowing the network to learn and make predictions.

These are just a few examples of the many applications of matrix multiplication. From engineering to physics, economics to social sciences, matrix multiplication provides a versatile tool for solving a wide array of problems.

Topics related to Matrix multiplication