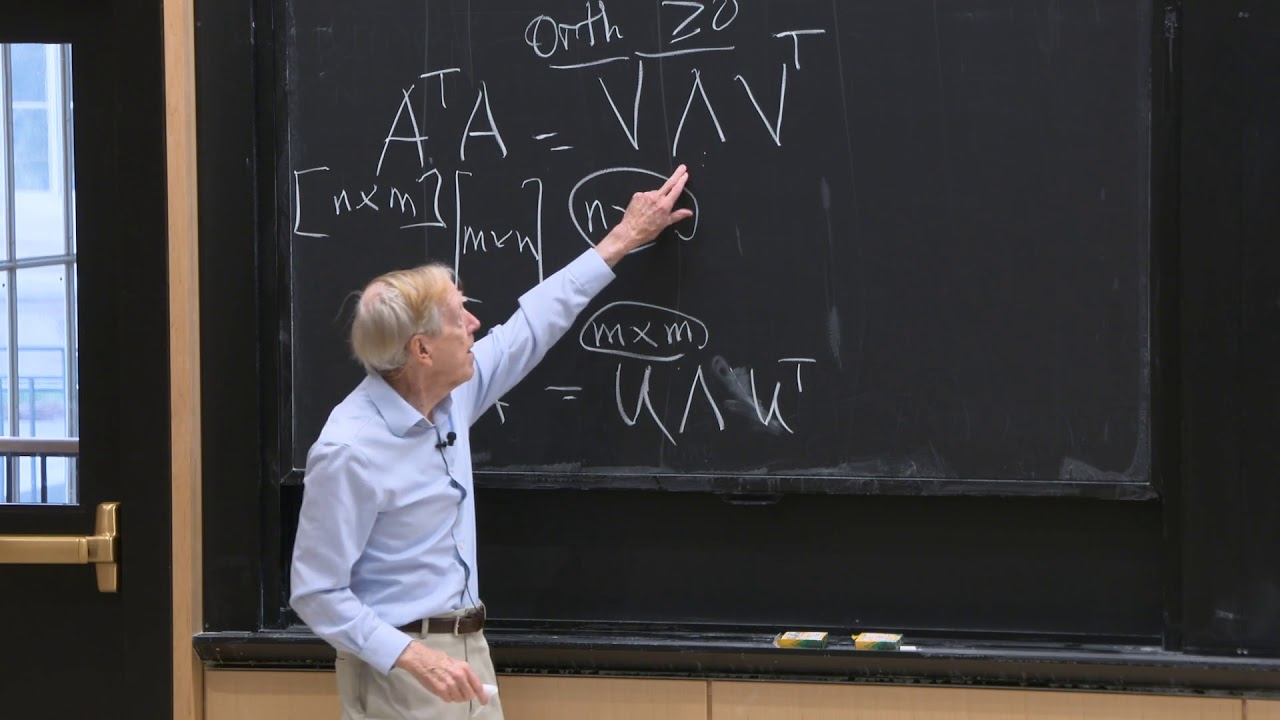Introduction to Singular Value Decomposition (SVD) and Mathematical Concepts and Background

Introduction to Singular Value Decomposition (SVD)

Singular Value Decomposition (SVD) is a mathematical factorization technique used to decompose a matrix into three separate matrices. It is commonly used in linear algebra and data analysis.

The singular value decomposition of a matrix A can be represented as A = UΣV^T, where U and V are orthogonal matrices and Σ is a diagonal matrix containing the singular values of A. The singular values in Σ are arranged in descending order, indicating their significance.

SVD provides a way to represent the original matrix in a concise and informative manner. It captures the underlying structure and relationships within the data by identifying the most important features or dimensions. This makes it useful for a wide range of applications, such as dimensionality reduction, image compression, recommendation systems, and data mining.

One important property of SVD is that it allows us to approximate a matrix with a lower rank by keeping only a certain number of singular values. This can be particularly helpful when dealing with large datasets, as it reduces computational complexity and storage requirements.

Additionally, SVD can be used for data preprocessing and noise reduction. By discarding or attenuating small singular values, it is possible to eliminate noise or outliers present in the data.

Overall, SVD is a powerful tool in linear algebra and data analysis, providing insights into the structure and relationships within datasets. Its applications range from numerical computations to machine learning, making it an essential technique in various fields.

Mathematical Concepts and Background

Mathematical Concepts and Background:

Singular Value Decomposition (SVD) is a fundamental concept in linear algebra and is used in many areas of mathematics, engineering, and computer science. It provides a way to break down a matrix into its constituent parts, revealing important information about the matrix’s properties and relationships.

In linear algebra, a matrix is a rectangular array of numbers arranged in rows and columns. The SVD of a matrix A is represented as A = UΣV^T, where U and V are orthogonal matrices, and Σ is a diagonal matrix with non-negative real values on the diagonal.

The orthogonal matrices U and V represent the transformations that occur during the decomposition process. U corresponds to the left singular vectors, and V corresponds to the right singular vectors. These vectors are orthogonal, meaning their dot product with each other is zero.

The diagonal matrix Σ contains the singular values of the matrix A. The singular values represent the scaling factors of the transformed vectors. They are typically arranged in descending order on the diagonal of Σ.

SVD has a wide range of applications, including dimensionality reduction, image compression, data analysis, and solving linear systems of equations. It can also be used to compute the pseudoinverse of a matrix, which is useful when dealing with matrices that are not invertible.

Overall, SVD is a powerful tool in linear algebra that allows us to gain insight into the structure and properties of matrices, and it has numerous practical applications in various fields.

The Process of Singular Value Decomposition

The process of Singular Value Decomposition (SVD) is a mathematical technique used to decompose a matrix into several components. It involves representing a matrix as the product of three separate matrices: U, Σ, and V* (V transpose).

1. Given an m × n matrix A, where m is the number of rows and n is the number of columns, the first step in SVD is to compute the singular values of A. Singular values are the square roots of the eigenvalues of A*A transpose.

2. Next, we calculate the left singular vectors of A, denoted by matrix U. These vectors span the column space of A and are orthogonal to each other.

3. We also compute the right singular vectors of A, denoted by matrix V. These vectors span the row space of A and are orthogonal to each other.

4. The diagonal matrix Σ is created using the singular values of A. The values are ordered in descending order, so the largest singular value corresponds to the first column of Σ.

5. Finally, the original matrix A can be reconstructed using the formula: A = UΣV*, where * denotes the transpose of the matrix V.

SVD has several applications in various fields, such as data compression, image processing, recommendation systems, and linear regression. It allows for the extraction of important features from a dataset and enables efficient manipulation and analysis of matrices.

Applications of SVD in Mathematics and Data Analysis

Singular Value Decomposition (SVD) is a powerful matrix factorization technique that finds applications in various fields of mathematics and data analysis. Some of its prominent applications are:

1. Dimensionality reduction: SVD can be used to reduce the dimensionality of a dataset while preserving the most important information. This is particularly useful in data analysis and machine learning, where high-dimensional data can be difficult to process and interpret.

2. Principal Component Analysis (PCA): PCA is a popular technique used for data analysis and feature extraction. It involves finding the principal components of a dataset, which are the orthogonal directions that capture the maximum variance. SVD enables efficient computation of PCA by decomposing the data matrix into its singular vectors and values.

3. Image compression: SVD is extensively used in image compression algorithms, such as JPEG. By representing images as a combination of singular vectors and values, SVD can efficiently compress the data by capturing the most significant features and discarding the less important ones.

4. Recommendation systems: SVD can be employed in collaborative filtering, a technique used in recommendation systems. By decomposing the user-item rating matrix using SVD, it becomes possible to identify latent factors underlying user preferences and make personalized recommendations based on these factors.

5. Data imputation: In situations where data is missing or incomplete, SVD can be used for data imputation. By decomposing the data matrix, missing entries can be estimated based on the low-rank approximation provided by the singular values and vectors.

6. Linear regression: SVD can also be used in linear regression problems to find the least-squares solution. By decomposing the design matrix, SVD enables efficient computation of the regression coefficients.

7. Data clustering: SVD can assist in data clustering algorithms by providing a low-dimensional representation of the data, making it easier to identify clusters and patterns.

Overall, SVD is a versatile tool that finds applications in various domains, including mathematics, data analysis, image processing, recommendation systems, and more. Its ability to uncover the underlying structure and dimensionality of data makes it an indispensable tool in modern data-driven research and analysis.

Advantages and Limitations of Singular Value Decomposition

Advantages of Singular Value Decomposition (SVD):

1. Dimensionality reduction: SVD is commonly used for reducing the dimensionality of a dataset by identifying the most important features. This can be especially useful when dealing with large datasets or when trying to visualize high-dimensional data.

2. Noise reduction: SVD can effectively filter out noise from data by removing the components with low singular values. This helps to improve the signal-to-noise ratio and enhance the quality of the data.

3. Data compression: SVD can compress data by representing it using a smaller number of singular values and their corresponding singular vectors. This can save storage space and speed up computations when dealing with large datasets.

4. Dealing with missing values: SVD can handle missing values in a dataset since it can fill in those gaps by estimating the missing values based on the available data.

Limitations of Singular Value Decomposition (SVD):

1. Computational complexity: The computational complexity of SVD is relatively high, especially for large datasets. This can make it computationally expensive and time-consuming, especially when dealing with real-time or online data.

2. Interpretability: The singular vectors obtained from SVD may not have a clear and intuitive interpretation. This can make it difficult to explain the factors or components that contribute to the data.

3. Sensitivity to outliers: SVD is sensitive to outliers in the data, meaning that the presence of outliers can significantly affect the accuracy of the decomposition. This can be problematic when dealing with datasets that contain noisy or erroneous observations.

4. Lack of scalability: SVD may not be scalable for datasets with millions or billions of records. The memory and computational requirements of SVD can become prohibitive for such large-scale datasets.

Overall, while SVD offers powerful capabilities for dimensionality reduction, noise reduction, and data compression, its limitations in terms of computational complexity, interpretability, sensitivity to outliers, and lack of scalability should be taken into consideration when deciding to use it for a particular application.

Topics related to Singular Value Decomposition (SVD)