Introduction to Gauss’s lemma and Explanation of Gauss’s lemma in mathematics

Introduction to Gauss’s lemma

Gauss’s lemma, also known as Gaussʼs lemma, is a fundamental result in number theory that relates the factorization properties of integers to the properties of their quadratic residues. The lemma is named after Carl Friedrich Gauss, a famous mathematician who made significant contributions to various fields of mathematics.

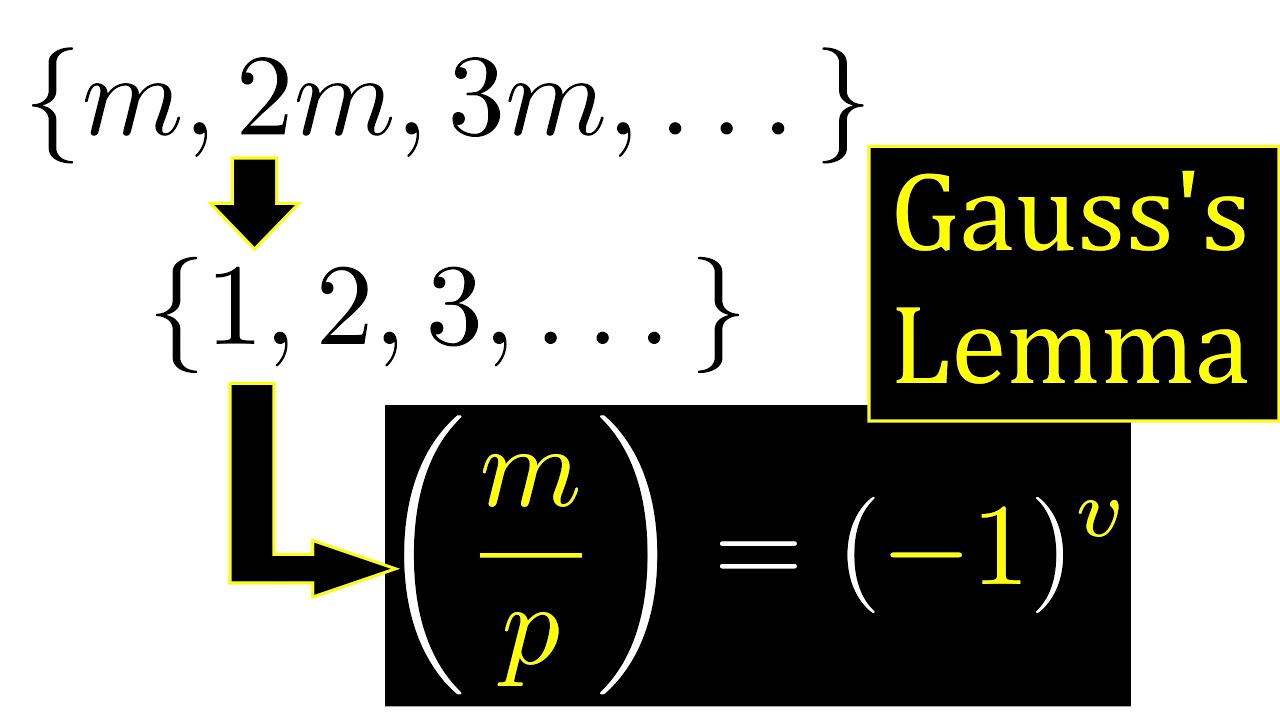
The lemma states that if a prime number p does not divide an integer a, then the Legendre symbol (a/p) is equal to 1 if a is a quadratic residue modulo p, and equal to -1 if a is a quadratic non-residue modulo p. The Legendre symbol is defined as a function that maps integers to these values based on whether they are quadratic residues or non-residues modulo a given prime.

Gauss’s lemma is useful in number theory, particularly in the study of quadratic forms, quadratic reciprocity, and the properties of prime numbers. It provides a way to determine whether an integer is a quadratic residue or non-residue modulo a prime without explicitly calculating the residues.

The lemma forms an important part of Gauss’s law of quadratic reciprocity, which establishes a relationship between the quadratic residues of two distinct primes. Gauss’s lemma serves as a crucial step in proving the quadratic reciprocity theorem.

Overall, Gauss’s lemma is a powerful tool in number theory that has numerous applications and implications in the study of primes, quadratic residues, and quadratic reciprocity. Its importance lies in its ability to connect the factorization properties of integers with the properties of their quadratic residues modulo prime numbers.

Explanation of Gauss’s lemma in mathematics

Gauss’s lemma is a result in number theory that provides a criterion for determining whether a polynomial in one variable with integer coefficients is irreducible (cannot be factored further).

The lemma states that if a polynomial with integer coefficients can be factored into two polynomials with rational coefficients, then it can also be factored into two polynomials with integer coefficients. In other words, if a polynomial can be written as a product of fractions, then it can be written as a product of integers.

This lemma is particularly useful in determining whether a polynomial with integer coefficients can be factored into linear factors or if it remains irreducible. It is often applied in the context of testing irreducibility of polynomials over the rational numbers or integers, or in factorization over the integers.

Gauss’s lemma is named after the renowned mathematician Carl Friedrich Gauss, who made significant contributions to many areas of mathematics, including number theory. His work on algebraic number theory led to the development of this important lemma.

Applications of Gauss’s lemma

Gauss’s lemma, named after the mathematician Carl Friedrich Gauss, has several important applications in different areas of mathematics. Some of the main applications include:

1. Quadratic reciprocity: Gauss’s lemma plays a crucial role in the proof of quadratic reciprocity, which is a fundamental result in number theory. Quadratic reciprocity establishes a relationship between the solvability of quadratic congruences and the residues of certain primes. It has applications in various areas, including cryptography and coding theory.

2. Polynomial irreducibility: Gauss’s lemma is often used to determine whether a polynomial is irreducible over a given field. The lemma states that if a polynomial with coefficients in a unique factorization domain (such as the integers or the ring of polynomials with coefficients in a field) can be factored into two polynomials with smaller coefficients, then it can also be factored in the same way within the domain itself.

3. Cyclotomic fields: In the theory of cyclotomic fields, Gauss’s lemma is used to prove that certain irreducible polynomials generate prime ideals. This is crucial for studying the unique factorization of elements in those fields and their extensions.

4. Diophantine equations: Gauss’s lemma is applied to establish conditions for the existence of integer solutions to certain types of Diophantine equations. It helps determine whether a given equation has solutions by considering the factorization of specific quantities involved.

5. Algebraic number theory: Gauss’s lemma is an essential tool for studying the unique factorization of primes in algebraic number fields. It allows for the characterization and analysis of prime elements, hence providing a deeper understanding of the arithmetic properties of those fields.

These are just a few examples of the broad range of applications for Gauss’s lemma in various branches of mathematics. Its utility in analyzing factorization, congruences, and the behavior of polynomials makes it a valuable tool in mathematical research and problem-solving.

Statement and proof of Gauss’s lemma

Statement of Gauss’s lemma:

Let $p$ be a prime number and $a$ be an integer not divisible by $p$. Then, the Legendre symbol $left(frac{a}{p}right)$ satisfies:

$$left(frac{a}{p}right) equiv a^{frac{p-1}{2}} pmod{p}$$

Proof of Gauss’s lemma:

Consider the set $A = {1, 2, 3, ldots, p-1}$ and define the set $B = {a cdot x mid x in A}$.

Since $a$ is not divisible by $p$, none of the elements of $B$ are divisible by $p$.

Let $r_1, r_2, ldots, r_k$ be the elements of $B$ which are less than or equal to $frac{p}{2}$, and let $s_1, s_2, ldots, s_l$ be the elements of $B$ which are greater than $frac{p}{2}$.

Thus, $k+l = p-1$ (as $1$ is not included in either set $B$ or $A$), and we can write $B$ as:

$$B = {r_1, r_2, ldots, r_k, s_1, s_2, ldots, s_l}$$

Now, for each $r_i$, there exists a unique $r_j$ such that $r_i cdot r_j equiv 1 pmod{p}$ (due to the property of inverses modulo $p$).

Similarly, for each $s_i$, there exists a unique $s_j$ such that $s_i cdot s_j equiv 1 pmod{p}$.

Multiplying all the elements of $B$ together, we have:

$$prod_{i=1}^{k} r_i cdot prod_{i=1}^{l} s_i equiv prod_{i=1}^{k} (r_i cdot r_j) cdot prod_{i=1}^{l} (s_i cdot s_j) equiv prod_{i=1}^{k} 1 cdot prod_{i=1}^{l} 1 equiv 1 pmod{p}$$

Since $r_1, r_2, ldots, r_k$ and $s_1, s_2, ldots, s_l$ represent the elements of sets $A$ and $B$ respectively, we get:

$$left(prod_{x in A} xright) cdot a^k equiv 1 pmod{p}$$

Taking the Legendre symbol on both sides, we obtain:

$$left(frac{a}{p}right) equiv left(prod_{x in A} xright)^{-1} cdot a^k equiv a^k equiv a^{frac{p-1}{2}} pmod{p}$$

This proves Gauss’s lemma.

Conclusion and significance of Gauss’s lemma in mathematics

Gauss’s lemma is a result in number theory that provides a criterion for determining whether a polynomial with integer coefficients is irreducible (i.e., cannot be factored into nontrivial polynomials with integer coefficients).

The lemma states that if a polynomial with integer coefficients can be factored into two non-constant polynomials with rational coefficients, then it can also be factored into two non-constant polynomials with integer coefficients.

This result is significant because it allows us to simplify the process of determining irreducibility of polynomials. Instead of having to search for all possible factorizations with rational coefficients, we can focus on finding factorizations with integer coefficients, which is often easier and more straightforward.

Gauss’s lemma has applications in various branches of mathematics, including algebraic number theory and algebraic geometry. It is an important tool for studying the properties of polynomials, and it provides a bridge between the worlds of rational and integer coefficients.

Overall, Gauss’s lemma is a fundamental result that simplifies the study of irreducibility of polynomials with integer coefficients and has wide-ranging implications in various areas of mathematics.

Topics related to Gaussʼs lemma