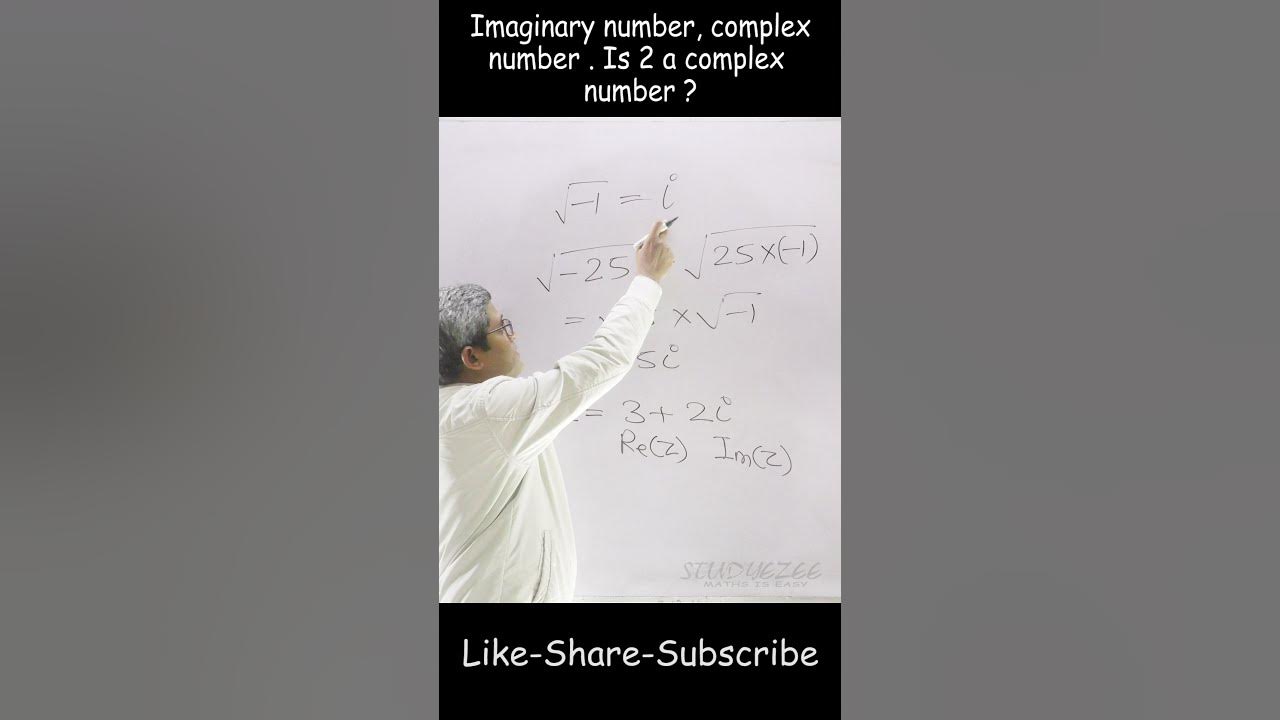Introduction to the Imaginary Part and Definition and Properties of the Imaginary Part

Introduction to the Imaginary Part

In mathematics, the imaginary part is a concept that is used for complex numbers. Complex numbers are numbers that consist of a real part and an imaginary part. The imaginary part is a multiple of the imaginary unit, denoted by the symbol “i” or “j”. The imaginary unit “i” is defined as the square root of -1.

The imaginary part of a complex number is expressed as a scalar multiple of “i”. For example, in the complex number 3 + 4i, the real part is 3 and the imaginary part is 4i. The imaginary part can be positive, negative, or zero, just like the real part.

The imaginary part of a complex number plays a crucial role in various branches of mathematics, physics, and engineering. It allows for the representation of quantities that involve a combination of real and imaginary components. For example, in electrical engineering, complex numbers are used to represent alternating currents, where the real part represents the resistive component and the imaginary part represents the reactive component.

The imaginary part also allows for the representation of complex solutions to equations that cannot be solved using only real numbers. For instance, the square root of a negative number is not a real number, but it can be represented using the imaginary part. This opens up new possibilities in mathematical equations and applications.

In summary, the imaginary part is an essential concept in complex numbers, providing a way to represent quantities that involve both real and imaginary components. It is used in various mathematical, physical, and engineering disciplines to solve complex problems and represent complex solutions.

Definition and Properties of the Imaginary Part

The imaginary part is a component of a complex number, which is a number that consists of a real part and an imaginary part. The imaginary part is represented by the letter “i” and it is defined as the coefficient of the imaginary unit “i”. The imaginary unit “i” is defined as the square root of -1.

For example, if we have a complex number z = a + bi, where “a” represents the real part and “b” represents the imaginary part, then the imaginary part is represented by “b”. The imaginary part can be positive, negative, or zero, depending on the value of “b”.

Properties of the imaginary part include:

1. Addition and subtraction: When adding or subtracting complex numbers, the real parts and imaginary parts should be combined separately. For example, (a + bi) + (c + di) = (a + c) + (b + d)i.

2. Multiplication: When multiplying complex numbers, the real parts and imaginary parts are multiplied separately, and the product of the imaginary parts is added to the product of the real parts. For example, (a + bi)(c + di) = ac + adi + bci – bd = (ac – bd) + (ad + bc)i.

3. Conjugate: The conjugate of a complex number z = a + bi is denoted as z* or z̅ and it is obtained by changing the sign of the imaginary part. For example, the conjugate of z = 3 + 2i is z* = 3 – 2i. The product of a complex number and its conjugate is always a real number.

4. Absolute value: The absolute value or modulus of a complex number z = a + bi is denoted as |z| and it is calculated as the square root of the sum of the squares of the real part and the imaginary part. For example, |z| = |a + bi| = sqrt(a^2 + b^2).

Overall, the imaginary part helps define the complex number and allows for various arithmetic operations and properties specific to complex numbers.

Operations Involving the Imaginary Part

The imaginary part of a complex number refers to the coefficient of the imaginary unit, denoted by “i”. In complex number notation, a complex number is written as a sum of its real and imaginary parts, expressed as a + bi, where “a” represents the real part and “b” represents the imaginary part.

Operations involving the imaginary part of a complex number can be performed similarly to operations involving real numbers. Here are some common operations involving the imaginary part:

1. Addition/subtraction: When adding or subtracting complex numbers, the real parts and imaginary parts should be combined separately. For example, (2 + 3i) + (4 + 2i) would result in (2 + 4) + (3 + 2)i = 6 + 5i.

2. Multiplication: To multiply complex numbers, you can use the distributive property. For example, (2 + 3i) * (4 + 2i) would result in (2 * 4 – 3 * 2) + (2 * 3 + 4 * 3)i = 8 – 6 + 6i + 12i = 2 + 18i.

3. Division: Division of complex numbers involves multiplying the numerator and denominator by the complex conjugate of the denominator. The complex conjugate of a number a + bi is a – bi, where a and b are real numbers. For example, (6 + 2i) / (4 + 3i) can be simplified by multiplying numerator and denominator by the conjugate of the denominator: [(6 + 2i) * (4 – 3i)] / [(4 + 3i) * (4 – 3i)] = (24 – 18i + 8i – 6i^2) / (16 – 9i^2) = (30 – 10i) / 25 = (6 – 2i) / 5.

These are just a few examples of operations involving the imaginary part of complex numbers. The principles remain the same for more complex calculations involving imaginary parts.

Applications of the Imaginary Part in Mathematics

The imaginary part of a complex number plays a significant role in various areas of mathematics. Some applications include:

1. Complex Analysis: In complex analysis, the imaginary part helps define important concepts like harmonic functions, Cauchy-Riemann equations, and conformal mappings.

2. Trigonometry: The imaginary part of a complex number is closely related to trigonometry. When representing complex numbers in polar form, the imaginary part corresponds to the sine component of the angle.

3. Signal Processing: The imaginary part is used in signal processing to analyze and manipulate complex signals. It helps in understanding the phase and frequency components of a signal.

4. Quantum Mechanics: Complex numbers and their imaginary parts are extensively used in quantum mechanics. The probability amplitudes that describe the behavior of particles are complex numbers, and the imaginary part represents the phase of these amplitudes.

5. Differential Equations: The imaginary part is often involved in solving differential equations. For example, when finding solutions to equations with oscillatory behavior, the imaginary part corresponds to the exponential decay or growth terms depending on the sign.

6. Fourier Analysis: The imaginary part is crucial in Fourier analysis, where complex exponentials are used to represent periodic functions. The imaginary part helps determine the amplitude and phase of the individual frequency components.

7. Electrical Engineering: The imaginary part is used to represent the reactive component of impedance in electrical circuits, which is crucial in understanding the behavior of capacitors and inductors.

These are just a few examples, highlighting the broad range of applications for the imaginary part in mathematics. It is a fundamental concept and finds use in various fields of study.

Conclusion and Significance of the Imaginary Part

The imaginary part of a complex number represents the vertical component of the number in the complex plane. It is denoted by the letter “i” and is multiplied by a real number to give the vertical displacement of the complex number.

The significance of the imaginary part lies in its role in complex analysis and applications in various fields. Some key points to consider include:

1. Representation of complex numbers: The imaginary part, along with the real part, helps in representing a complex number as a combination of a real number and an imaginary number.

2. Complex conjugates: The imaginary part is crucial for finding the complex conjugate of a complex number. The conjugate of a complex number is obtained by changing the sign of the imaginary part, while keeping the real part unchanged.

3. Polar representation: The imaginary part plays a significant role in representing complex numbers in polar form. In polar form, a complex number is expressed as a magnitude and an angle. The imaginary part helps determine the angle at which the complex number is located in the complex plane.

4. Characterizing complex functions: In complex analysis, the imaginary part is used to study and characterize complex functions, including their behavior, singularities, and properties. It helps in understanding how the complex function maps points in the complex plane.

5. Applications in physics and engineering: The imaginary part is widely used in physics and engineering applications, such as in the analysis of electrical circuits, control systems, quantum mechanics, signal processing, and wave propagation. It allows for the representation and manipulation of quantities that involve both magnitude and phase information.

In conclusion, the imaginary part of a complex number plays a fundamental role in complex analysis and has significant applications in various fields. It helps in representing complex numbers, finding complex conjugates, characterizing complex functions, and is essential in polar representations and various physics and engineering applications.

Topics related to Imaginary part