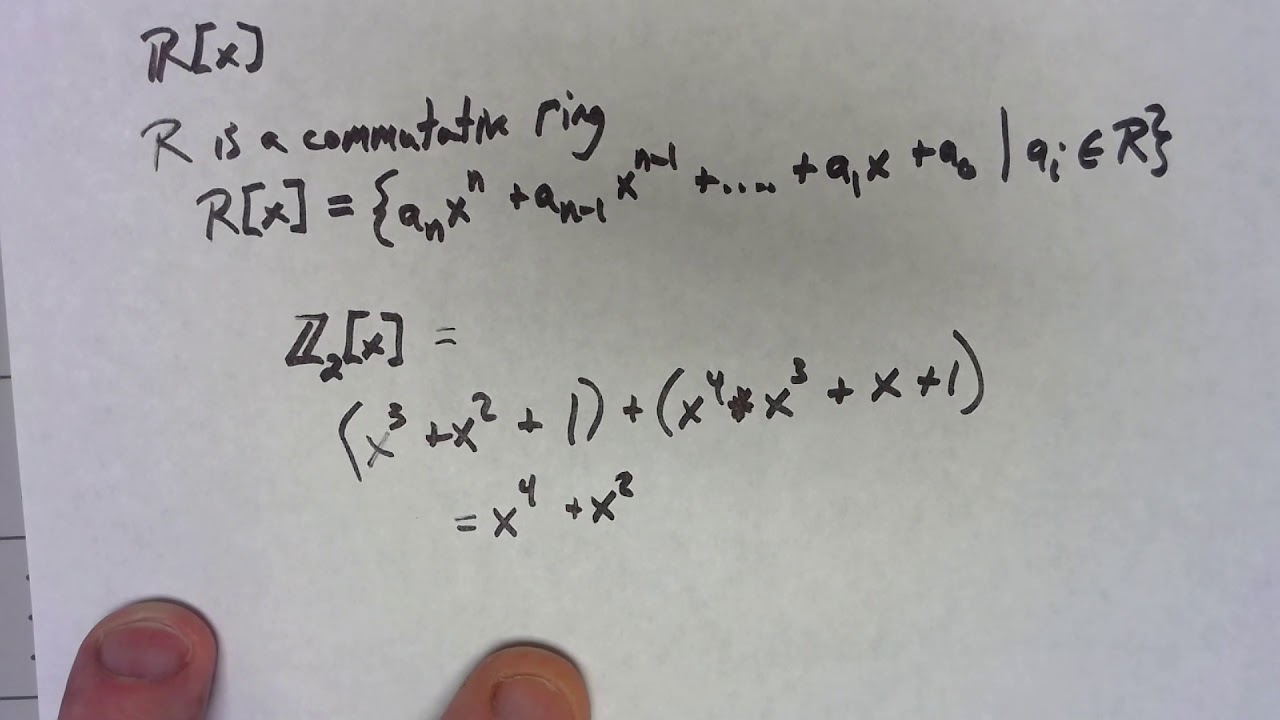Introduction to Polynomial Rings and Definition and Structure of Polynomial Rings

Introduction to Polynomial Rings

A polynomial ring can be defined as an algebraic structure built upon a set of polynomials with coefficients from a given ring. It is constructed by formalizing the operations of addition and multiplication on polynomials.

In a polynomial ring, the polynomials can have variables and coefficients, and the variables can be combined using the operations of addition and multiplication. The variables often represent indeterminates, which means that they do not have specific values assigned to them.

The ring from which the coefficients are taken defines the underlying structure of the polynomial ring. The ring can be the set of integers, the set of real numbers, or any other ring with defined addition and multiplication operations.

To form a polynomial ring, we start with a set of polynomials with coefficients from the given ring. We then define the addition and multiplication operations on these polynomials in a way that preserves the properties of the coefficients’ ring.

For example, in the polynomial ring of polynomials with coefficients from the set of real numbers, we can add and multiply polynomials just as we would with real numbers. Addition is done by adding the coefficients of corresponding terms, and multiplication is done by multiplying the terms and then adding the products.

The polynomial ring is often denoted as R[x], where R represents the ring of coefficients, and x represents the variable. The elements of the polynomial ring are the polynomials constructed from the coefficients and variables.

Polynomial rings are important in various fields of mathematics, including algebra, number theory, and algebraic geometry. They provide a powerful tool for studying and solving problems involving equations and polynomials. Additionally, polynomial rings have connections to other algebraic structures, such as ideals, factorization, and polynomial functions.

Definition and Structure of Polynomial Rings

A polynomial ring is a mathematical structure that consists of polynomials with coefficients from a given ring. In other words, it is an algebraic object formed by combining elements of a ring with variables and their powers.

Formally, the polynomial ring over a ring R in one variable x is denoted by R[x]. It is defined as the set of all formal expressions of the form:

f(x) = a_n x^n + a_{n-1} x^{n-1} + … + a_1 x + a_0

where the coefficients a_i belong to the ring R, and n is a non-negative integer. The elements of R[x] are called polynomials, and the coefficients a_i are often referred to as the “terms” of the polynomial.

The addition of polynomials in R[x] is defined term-wise, meaning that two polynomials are added by adding their corresponding coefficients. Similarly, multiplication of polynomials is done by the distributive property, multiplying each term of one polynomial with each term of the other.

The polynomial ring also has a well-defined identity element, which is the constant polynomial 1. This means that every polynomial can be multiplied by 1 without changing its value.

Additionally, polynomial rings can be extended to include multiple variables and higher dimensions by introducing additional variables and their powers.

Polynomial rings have many important properties and are widely used in various areas of mathematics, including algebra, number theory, and algebraic geometry. They provide a powerful tool for studying and manipulating polynomials, which appear in many mathematical problems and applications.

Operations and Properties of Polynomial Rings

In mathematics, a polynomial ring is a structure that allows us to perform operations and explore properties related to polynomials.

The ring is denoted as R[x], where R is a ring and x is an indeterminate (a variable that is not assigned any specific value). The elements of the polynomial ring are polynomials in x with coefficients from R.

The operations defined in a polynomial ring include addition, subtraction, and multiplication of polynomials. Addition and subtraction are performed by combining like terms, that is, terms with the same degree of x. Multiplication involves the distribution of terms, so that every term in one polynomial is multiplied by every term in the other polynomial.

One important property of polynomial rings is closure under addition and multiplication. This means that adding or multiplying two polynomials always results in another polynomial.

Another property is the commutative property of addition and multiplication. This means that the order in which we add or multiply polynomials does not affect the result.

The polynomial ring also has an identity element for addition, which is the zero polynomial (a polynomial with all coefficients equal to zero). This means that adding the zero polynomial to any other polynomial does not change the result.

In terms of multiplication, the polynomial ring has an identity element called the constant polynomial 1. This means that multiplying any polynomial by the constant polynomial 1 does not change the polynomial.

The polynomial ring is also an integral domain, which means that it has no zero divisors. In other words, if a polynomial multiplied by another polynomial equals the zero polynomial, then at least one of the polynomials must be the zero polynomial itself.

Additionally, the polynomial ring is also a commutative ring, meaning that multiplication is commutative, and it satisfies the distributive property, allowing us to distribute multiplication over addition.

These are just some of the operations and properties of polynomial rings. The study of these rings is essential in algebra and has many applications in various areas of mathematics.

Examples and Applications of Polynomial Rings

Polynomial rings have numerous examples and applications in various fields of mathematics. Here are a few:

1. Algebraic Geometry: Polynomial rings are extensively used in the study of algebraic varieties and their properties. In this context, the ring of polynomials over a field serves as the coordinate ring for the corresponding affine variety.

2. Number Theory: Polynomial rings play a fundamental role in the study of Diophantine equations, which are equations involving integer solutions. By considering polynomial equations over the ring of integers, one can investigate properties of prime numbers, factorization, and other number-theoretic phenomena.

3. Computer Algebra: Polynomial rings are widely used in computer algebra systems for symbolic computations. These systems employ polynomial rings to perform calculations involving algebraic expressions, solve equations, compute derivatives and integrals, and perform other mathematical operations.

4. Coding Theory: Polynomial rings are essential in coding theory, which deals with error-detecting and error-correcting codes. Polynomial rings are used to construct cyclic codes, a class of linear error-correcting codes that exhibit specific algebraic properties.

5. Cryptography: Certain cryptographic techniques rely on properties of polynomial rings. For example, polynomial rings are used in polynomial-based encryption schemes like the Learning with Errors (LWE) problem, which provides a basis for secure communication and encryption protocols.

6. Approximation Theory: Polynomial approximation is a common method for approximating functions by polynomials. By using polynomial rings, mathematicians can construct and analyze polynomial approximations and understand their convergence properties.

7. Optimization: Polynomial programming involves optimizing polynomial functions subject to certain constraints. Polynomial rings provide a mathematical framework for modeling and solving optimization problems, enabling researchers to find optimal solutions in various fields such as operations research, engineering, and economics.

8. Dynamical Systems: Polynomial rings are used in the study of dynamical systems, which involve the evolution of variables over time. By associating polynomial equations with dynamical systems, mathematicians can analyze the behavior, stability, and equilibrium points of these systems.

These are just a few examples among many that highlight the diverse applications and significance of polynomial rings in different branches of mathematics and its applications.

Conclusion and Further Reading

In conclusion, the polynomial ring is a fundamental concept in algebra that allows us to study and manipulate polynomials in a systematic way. It provides a framework for performing arithmetic operations on polynomials, including addition, subtraction, multiplication, and division. Polynomial rings also have important properties such as being a commutative and unitary ring.

Further reading on polynomial rings can be done in various algebra textbooks. Some recommended readings include:

1. “Abstract Algebra” by David S. Dummit and Richard M. Foote: This comprehensive textbook covers a wide range of algebraic concepts, including polynomial rings.

2. “Introduction to Commutative Algebra” by Michael Atiyah and Ian Macdonald: This book provides a detailed introduction to commutative algebra, which includes a thorough coverage of polynomial rings.

3. “Polynomial Rings” by Paul Cohn: This book focuses specifically on polynomial rings and provides a deep understanding of their properties and applications.

4. “Ideals, Varieties, and Algorithms” by David Cox, John Little, and Donal O’Shea: This book combines algebraic theory with computational methods and provides a practical approach to polynomial rings.

These books will provide you with a solid foundation in polynomial rings and help you explore their various applications in algebra and related fields.

Topics related to Polynomial ring